Zbadaj liczbę rozwiązań danego równania w zależności od wartości parametru m.
qwerty: Zbadaj liczbę rozwiązań danego równania w zależności od wartości parametru m.
a) |x−4| + |2+x| = m
b) |5−x| − |x−2| = m
28 lut 15:20
chichi:
f(x) = |x − 4| + |2 + x|, szkicuj wykres funkcji f i analiza wykresu

28 lut 16:00
Mila:
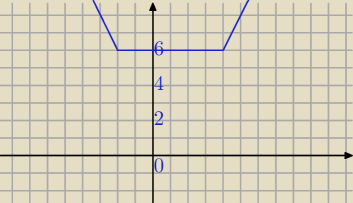
a)
|x−4|+|2+x|=|x−4|+|−2−x|≥|x−4−2−x|=6
dokończ
28 lut 16:46
Mila:
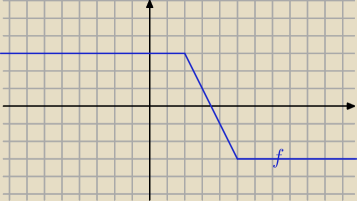
b) |5−x|−|x−2|=|x−5|−|x−2|
f(x)=|x−5|−|x−2|
28 lut 16:50
qwerty: jak można to rozwiązać bez analizowania wykresu funkcji?
1 mar 20:54
chichi:
analizując przypadki

1 mar 21:43
Jolanta: Chichi a możesz to rozwiązać ? Bardzo chciałabym przypomniec sobie jak to się robilo
1 mar 21:52
Jolanta: Czy dobrze pamiętam,ze na osi zaznaczam x= 4 i x=−2 i rozwiązuje w przedziałach
1) od −∞ do −2
2) od −2 do 4
3) od 4 do ∞
1 mar 21:59
chichi:
tak jest

1 mar 22:20
Jolanta:
1)−x+4−2−x=m
−2x+2=m
2)−x+4+2+x=m
6=m
3) x−4+2+ x=m
2 x−2 =m
1 mar 22:35
Jolanta: Mogłabym prosić o odpowiedz taka słowna Nie pamiętam parametrow
1 mar 22:40
qwerty: dlaczego dla samego m=8 jest nieskończenie wiele rozwiązań?
1 mar 22:48
qwerty: znaczy się m=6
2 mar 03:26
Mila:
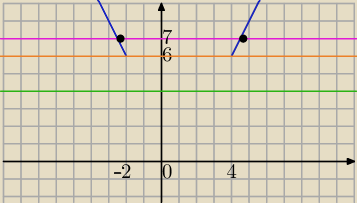
f(x)=|x−4|+|2+x|
(*) |x−4|+|2+x|=m
g(x)=m funkcja stała, m∊R
f(x)=g(x) punkty przecięcia wykresów
1) m<6 np. m=4 brak rozwiązań
2)
m=6 dla każdego x∊<−2,4> wykresy pokrywają się⇔masz nieskończenie wiele rozwiązań.
Każda liczba z tego przedziału spełnia równanie (*)
3) m>6
np. m=7
wykresy przecinają się w dwóch punktach⇔
dla m>6 równanie :
|x−4|+|2+x|=m ma dwa rozwiązania
2 mar 15:13
Jolanta: Dziękuję za wyjaśnienia

2 mar 20:37
Mila:

2 mar 22:00

 a)
|x−4|+|2+x|=|x−4|+|−2−x|≥|x−4−2−x|=6
dokończ
a)
|x−4|+|2+x|=|x−4|+|−2−x|≥|x−4−2−x|=6
dokończ
 b) |5−x|−|x−2|=|x−5|−|x−2|
f(x)=|x−5|−|x−2|
b) |5−x|−|x−2|=|x−5|−|x−2|
f(x)=|x−5|−|x−2|


 f(x)=|x−4|+|2+x|
(*) |x−4|+|2+x|=m
g(x)=m funkcja stała, m∊R
f(x)=g(x) punkty przecięcia wykresów
1) m<6 np. m=4 brak rozwiązań
2)
m=6 dla każdego x∊<−2,4> wykresy pokrywają się⇔masz nieskończenie wiele rozwiązań.
Każda liczba z tego przedziału spełnia równanie (*)
3) m>6
np. m=7
wykresy przecinają się w dwóch punktach⇔
dla m>6 równanie :
|x−4|+|2+x|=m ma dwa rozwiązania
f(x)=|x−4|+|2+x|
(*) |x−4|+|2+x|=m
g(x)=m funkcja stała, m∊R
f(x)=g(x) punkty przecięcia wykresów
1) m<6 np. m=4 brak rozwiązań
2)
m=6 dla każdego x∊<−2,4> wykresy pokrywają się⇔masz nieskończenie wiele rozwiązań.
Każda liczba z tego przedziału spełnia równanie (*)
3) m>6
np. m=7
wykresy przecinają się w dwóch punktach⇔
dla m>6 równanie :
|x−4|+|2+x|=m ma dwa rozwiązania

