funkcja kwadratowa pr
silnia: Dana jest funkcja f(x)=|x(x−2)−3|. Wskaż zdanie fałszywe:
prawidlowa odp to Równanie f(x)=4ma dwa rozwiązania.
ja zrobilem rozpisanie na przypadki
f(x)=|x(x−2)−3| = |x
2−2x−3|
| | ⎧ | x2−2x−3 gdy x≥0 | |
| f(x)= | ⎨ | |
|
| | ⎩ | −x2+2x−3 gdy x<0 | |
i wyszla mi odpowiedz, ze funkcja rosnie dla przedzialu <−1,1>, czy to poprawny sposob
rozwiazania?
27 lut 19:54
wredulus_pospolitus:
f(x) = |x2−2x−3| = |(x+1)(x−3)| <−−−− z takiej postaci lepiej naszkicować wykres
27 lut 20:24
silnia: Funkcja f maleje dla (−∞, −1>
Funkcja f rośnie dla <−1,1>
Równanie f(x)=4 ma dwa rozwiązania
Funkcja f ma dwa miejsca zerowe.
To ktora odpowiedz jest poprawna? Bo po narysrowaniu pasuje mi d i a, a prawdilowa odp to c.
27 lut 20:39
wredulus_pospolitus:
A jakie są odpowiedzi?
27 lut 20:40
chichi:
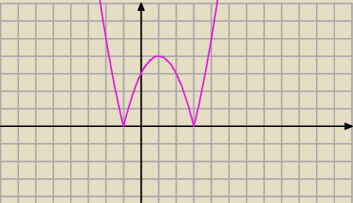
27 lut 20:41
wredulus_pospolitus:
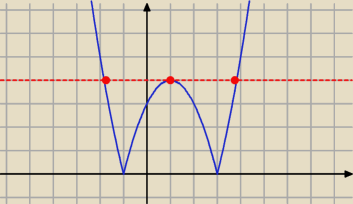
f(x) = 4 ma dokładnie 3 rozwiązania

27 lut 20:42
wredulus_pospolitus:
tak więc ta odpowiedź (czyli (c)) będzie odpowiedzią FAŁSZYWĄ, czyli tą odpowiedź zaznaczasz

27 lut 20:43

 f(x) = 4 ma dokładnie 3 rozwiązania
f(x) = 4 ma dokładnie 3 rozwiązania 
