dlaczego funkcja f(𝑥)= x -|𝑥| po przesunięciu 𝑔(𝑥)=𝑓(|𝑥|)
kkk:
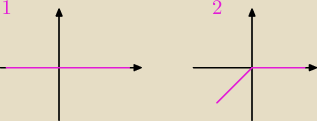
cześć, dlaczego funkcja f(𝑥)= x −|𝑥| po przesunięciu 𝑔(𝑥)=𝑓(|𝑥|) wygląda tak jak na 2
rysunku?
26 lut 20:42
kkk: rysunki mają być odwrotnie, pomyliłam się (1 dotyczy f(𝑥)= x −|𝑥, a drugi jest po jej
przesunięciu)
26 lut 20:43
kkk:
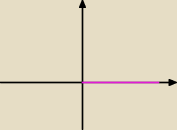
Wiem, że jak jest IxI to x ≥ 0, ale zrobiłabym ten wykres jakoś tak. Mógłby mi ktoś wytłumaczyć
dlaczego moja wersja jest zła?
26 lut 20:45
Mila:
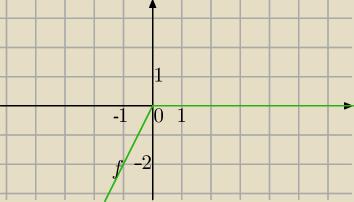
1) f(𝑥)= x −|𝑥|
a) x≥0 to f(x)=x−x=0
x<0 to f(x)=x−(−x)=2x
2)
g(x)=f(|x|)=|x|−|x|=0 wykres (1) z 20:42
26 lut 20:49
Aruseq: Przekształcenie y=f(|x|) oznacza, że prawa strona wykresu zostaje taka sama i odbijamy ją
symetrycznie względem osi OY na lewą stronę
26 lut 20:49
kkk:
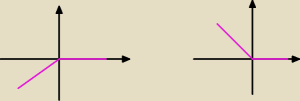
Czyli danie tego x do wartości bezwzględnej nie oznacza, że muszę przenieść te x, które były
ujemne tak aby były dodatnie?
Miałam też przykład 𝑔(𝑥) = |𝑓(𝑥)| i tutaj przeniosłam ujemne y żeby były dodatnie i wynik
mi się zgadza. Z f(|x|) nie można tak tego interpretować?
dodaje jeszcze wykres jaki zrobiłam dla tej sytuacji z |𝑓(𝑥)| (nie oznaczam na nich wartości
bo chodzi mi o sam układ)
26 lut 21:03
Mila:
kkk, przeczytaj wyjaśnienie 20:49, a potem praktyczną radę Aruseq.
26 lut 22:54
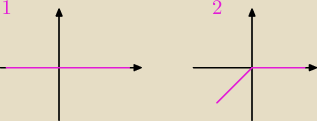 cześć, dlaczego funkcja f(𝑥)= x −|𝑥| po przesunięciu 𝑔(𝑥)=𝑓(|𝑥|) wygląda tak jak na 2
rysunku?
cześć, dlaczego funkcja f(𝑥)= x −|𝑥| po przesunięciu 𝑔(𝑥)=𝑓(|𝑥|) wygląda tak jak na 2
rysunku?
 Wiem, że jak jest IxI to x ≥ 0, ale zrobiłabym ten wykres jakoś tak. Mógłby mi ktoś wytłumaczyć
dlaczego moja wersja jest zła?
Wiem, że jak jest IxI to x ≥ 0, ale zrobiłabym ten wykres jakoś tak. Mógłby mi ktoś wytłumaczyć
dlaczego moja wersja jest zła?
 1) f(𝑥)= x −|𝑥|
a) x≥0 to f(x)=x−x=0
x<0 to f(x)=x−(−x)=2x
2)
g(x)=f(|x|)=|x|−|x|=0 wykres (1) z 20:42
1) f(𝑥)= x −|𝑥|
a) x≥0 to f(x)=x−x=0
x<0 to f(x)=x−(−x)=2x
2)
g(x)=f(|x|)=|x|−|x|=0 wykres (1) z 20:42
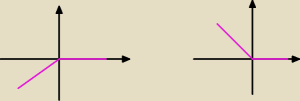 Czyli danie tego x do wartości bezwzględnej nie oznacza, że muszę przenieść te x, które były
ujemne tak aby były dodatnie?
Miałam też przykład 𝑔(𝑥) = |𝑓(𝑥)| i tutaj przeniosłam ujemne y żeby były dodatnie i wynik
mi się zgadza. Z f(|x|) nie można tak tego interpretować?
dodaje jeszcze wykres jaki zrobiłam dla tej sytuacji z |𝑓(𝑥)| (nie oznaczam na nich wartości
bo chodzi mi o sam układ)
Czyli danie tego x do wartości bezwzględnej nie oznacza, że muszę przenieść te x, które były
ujemne tak aby były dodatnie?
Miałam też przykład 𝑔(𝑥) = |𝑓(𝑥)| i tutaj przeniosłam ujemne y żeby były dodatnie i wynik
mi się zgadza. Z f(|x|) nie można tak tego interpretować?
dodaje jeszcze wykres jaki zrobiłam dla tej sytuacji z |𝑓(𝑥)| (nie oznaczam na nich wartości
bo chodzi mi o sam układ)