Trójkąt wpisany Konrad: A(6, −5) jest jednym z wierzchołków trójkąta wpisanego w okrąg (x−3)² + (y+1)² = 25 Oblicz pole trójkąta jeśli wiadomo że prosta 7x −y −22= 0 jest jego osią symetrii I liczyłem tak i chciałem policzyć s bo ta prosta 7x− y −22 przecina koło w c1 i C2 i chciałem policzyć odległości od tych c od S i po prostu pole bo to wysokości ale coś nie WYCHODZI Jak by ktoś mógł coś poradzić https://files.fm/u/dhma3ccmg

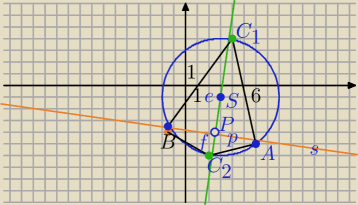
Mila: Nie mogę odczytać linka A(6, −5) 7x −y −22= 0 k: y=7x−22 O=(3,−1) − wsp. środka okręgu 1) Prostopadła do k i przechodząca przez punkt C

	1		1
s: y=−		x+b i −5=−		*6+b
	7		7

	23
b=−
	6

	1		23
s: y=−		x−
	7		6

|C₁C₂|=10 średnica ,Punkt S∊k

	|7*6+5−22|		25		5
|AP|=d(A,k)=		=		=
	√72+12		5√2		√2

	10
|AB|=
	√2

2) ΔC₁AC₂ i ΔC₁BC₂− Δprostokątne p²=e*f

	25
e*f=
	2

e+f=10

	5		5
e=5+		, f=5−
	√2		√2

licz pola ΔABC₁ i ΔABC₂

Eta: 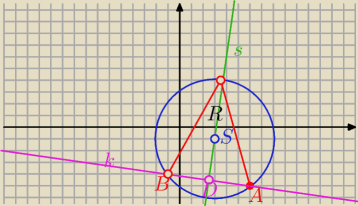2 sposób

	1
P(ABCD)=		|AB|*(|SD|+R)
	2

R=5 , S=(6,−5) s: 7x−y−22=0 k ⊥s i A∊k k: (x−6)+7(y+5)=0 k: x+7y+29=0

1
	|AB| = d −− odległość punktu A od prostej s
2

i |SD|= d−−−− odległość punktu S od prostej k

1		|42+5−22|		5√2
	|AB|=		=
2		√50		2

	|3−7+29|		5√2
|SD|=		=
	√50		2

PΔ= .............

Eta: Oczywiście chochlik ........ ma być S(3,−1)