wykaż, że Asiula: wykaż, że dla tg alfa = √5/2 (pierwiastek z 5 podzielić na 2 (sinα−√5cosα) podzielić na 6(cos²α−sin²α)=√5/2 pomocy

siula:

	√5		sinα		√5
tgα =		⇒		=		⇒ sinα = ...
	2		cosα		2

oraz sin²α = 1 − cos²α

sinα − √5cosα		√5
	=		⇒ ....
6(cos2α − sin2α)		2

Asiula: no ja właśnie tego ostatniego nie mogę przebrnąć, wydaje mi sie, że popełniam cały czas ten sam bład − nie mogę wyjśc na to √5/2 mogłby mi to ktoś rozpisać...... pliiis .....

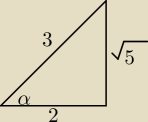
an: Przepisz to zadanie co tam trzeba wykazać

Asiula: wykaż, że dla tgα=√5/2 (sinα−√5cosα) podzielić na 6(cos2α−sin2α)=√5/2 geometrycznie na trojkącie super mi wyszło ))) ale mam jakiś problem z wyprowadzeniem tego algebraicznie (sinα−√5cosα) podzielić na 6(cos2α−sin2α)=√5/2 sinα= √5/2 cosα sin²α=1−cos² podstawiłam za sinusy √5/2 cosα−√5cosα podzielić na 6(cos²α−(1−cos²α) i ma wyjść =√5/2 a mnie nie wychodzi i utknęłam... coś robię cały czas źłe

an:

	√5
sinα=		cosα |podnosimy do kwadratu
	2

i korzystając z sin²α + cos²α=1

	4
cos2α=
	9

i dalej ..L=P

Asiula: Super! Bardzo dziękuję.......... Nie wiem dlaczego tok myślenia miałam zupełnie inny Ale i tak czasowo − metoda geometryczna wymiata Pozdrawiam

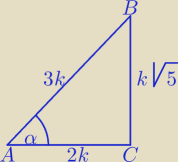
Mila: Asiula , ułamki piszemy za pomocą dużej litery U U{licznik} {mianownik} pomijając spację między klamrami. W pewnych sytuacjach korzystając z metody geometrycznej lepiej oznaczać tak, jak na rysunku. k>0 c=3k

	√5
sinα=
	3

	2
cosα=
	3