wyzancz m fabian: Wyznacz wszystkie wartości parametru m, dla których iloczyn wszystkich rozwiązań równania |x²+2x−3|= m jest liczbą dodatnią.

wredulus_pospolitus: |x²+2x−3| = |(x+3)(x−1)| = m jeżeli iloczyn ma być dodatni −−− to mamy: 1. 2 rozwiązania gdy Sprawdź czy mogą być tego samego znaku (podpowiedź − nie mogą) 2. 3 rozwiązania gdy Sprawdź czy będą wtedy dwa ujemne i jeden dodatni (tak będzie) 3. 4 rozwiązania gdy Sprawdź kiedy dokładnie dwa będą ujemne i dokładnie dwa dodatnie Do dzieła

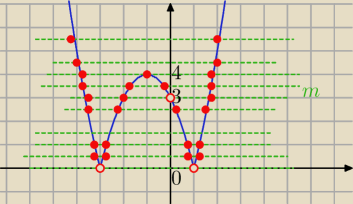
ada: dla m ∊(0,3) dwa ujemne i dwa dodatnie więc iloczyn dodatni dla m=4 dwa juemne i jeden dodatni więc iloczyn dodatni i tyle odp : m∊(0,3) U{4}

Kuba: rozwiazanie ady jest ok, jednak 4 nie pasuje. Podstaw 4. |x²+2x−3|=4 x²+2x−3=4 lub x²+2x−3=−4 x²+2x−7=0 lub x²+2x−1=0 ze wzorów viete'a (x+1)²=0 c/a= −7/1=−7 x=−1 podwójne iloczyn pierwiastków −7*(−1)*(−1)=−7 Odpada. odp m∊(0,3)

mat3: x₁*x₂= −7 i x₃= −1 więc: x₁*x₂*x₃= −7*(−1)= 7 >0 pasuje odp: m∊(0,3)U{4}