16 lut 11:54
chichi:
przygotowujesz się do konkursów?
16 lut 13:10
Paulina: Da się to jakoś rozwiązać czy raczej skomlikowane?
16 lut 15:02
Mila:
Da się. Trzeba coś dorysować.
16 lut 15:13
Paulina: No a co dorysować bo jakoś niestety nie widze
16 lut 15:15
Mila:
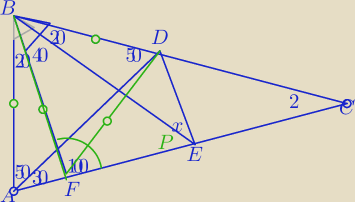
Podpowiedź.
Licz dalej kąty.
16 lut 16:02
Paulina: Ok dzieki popróbuję
16 lut 16:06
Mila:
Powodzenia.
16 lut 16:15
16 lut 17:09
Mariusz:
A gdyby ba boku DE dorysować trójkąt równoboczny ?
ale wtedy trzeba by pokazać że wysokość takiego trójkąta jest zawarta w boku BE
16 lut 17:39
Mila:
Mariusz wystarczy obliczyć kąty − rys.16:02
17 lut 14:39
Mariusz:
Mila na twoim rysunku ΔFED gdzie FD = FE
i wtedy widać jaka powinna być miara kąta
Nie zaznaczyłaś tego bo byłoby za łatwo ?
17 lut 18:14
Mariusz:
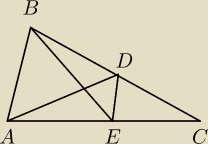
Bez dorysowywania to można by nanieść układ współrzędnych
i wtedy współczynnik kierunkowy to tangens kąta nachylenia do osi odciętych
Współrzędne punktów A oraz C można by sobie obrać dowolnie na osi odciętych
Współrzędne punktów B,D,E można otrzymać z układu równań
Miarę kąta BEA dostajemy z sumy miar kątów w trójkącie
Miarę kąta CED dostaniemy licząc współczynnik kierunkowy prostej DE
Ponadto ∡BEA + ∡x + ∡CED = 180°
bo AC linia prosta
17 lut 19:26
Mila:
Nie zaznaczyłam, bo jest to podpowiedź dla Pauliny.
18 lut 14:41
Mariusz :
Ta tyle że nie tylko Paulina ogląda ten wątek
No ale twój pupilek napisał że to zadanie konkursowe
"chichi jakie piękne rozwiązanie, krótkie"
Jeżeli chodzi o mój pomysł z 17 lut 2023 19:26
to stosunkowo łatwo na niego wpaść i mimo iż wymaga on nieco obliczeń
to naniesienie układu współrzędnych sprawi że nie będzie to zadanie aż takie trudne
Mój rysunek nie odwzorowuje sytuacji z zadania bo kąt CED powinien być rozwarty
a tego z rysunku nie widać
18 lut 23:07
Mila:
Jeżeli ktoś ogląda, to może zapytać, dokończyć, skrytykować, nic nie pisać itp.
Po co ta ironia Mariuszu ?
Syntetyczne rozwiązania chichi są piękne. Zazdrościsz?
19 lut 00:55
Franek z fabryki szklanek: i tylko 50 linijek , to jest lekkie przegięcie ale w drugą stronę
Nie idź Mariusz tą drogą którą chodzi użytkownik jakub gurak z forum matematyka.pl , to jest
droga donikąd
22 lut 09:16
a7: to czy wiadomo jaką miarę ma w końcu x? bo ja się nie doliczylam....
22 lut 12:41
ite:
Z rozwiązania Mili można odczytać że 30o. W zapisach z fotosiku 8:37 taka wartość się nie
jeszcze nie pojawia, ale to chyba dopiero początek rozwiązania.
22 lut 13:32
22 lut 14:24
a7: a skąd wiadomo, że BF=FD?
22 lut 14:55
a7: i, że BF=BD?
22 lut 15:09
ite:
Zaraz pewnie zajrzy tu Mila, to wyjaśni, jak dodawała odcinki do wyjściowego rysunku.
Zwróć uwagę, że równość kilku odcinków wiąże się w tym rozwiązaniu z równością kątów.
22 lut 16:03
chichi:
to zadanie już kiedyś było na forum, rozw. które podała @
Mila 16 lut 16:02 wtedy
właśnie zaproponowałem, jeżeli komuś zechce się znaleźć ten wątek, to możliwe, że zostawiłem
tam bardziej szczegółowy opis do rozw.
22 lut 16:35
Mila:
a7
1) ΔAFB− Δ o kątach : 20o, 80o,80o zatem równoramienny
i
|AB|=|BF|
2)
ΔABD − Δ o kątach : 50o,80o, 50o zatem równoramienny
i
|AB|=|BD|=|BF
3)
ΔBFE−Δ o kątach : 40o,100o40o zatem równoramienny
i
|BF|=|FD|
4)
ΔBFD− trójkąt równoboczny
Policz dalej sama
22 lut 18:44
a7: Dziękuję Mila, spróbuję się jeszcze doliczyć tych 30o
22 lut 18:52
Mila:
Pisz w razie wątpliwości
Powodzenia.
22 lut 20:19
a7: Dziękuję
22 lut 22:23
chichi:
usuńcie to proszę, bo jego wpisy zrażają dzieci do geometrii
22 lut 23:43
ada:
22 lut 23:45
Likwidator:
USUNIĘTE
23 lut 01:06
chichi:
niech Bóg Ci to wynagrodzi dobry człowieku, krok dla dobra ludzkości, a zwłaszcza młodych
konkursowiczów, dobrej nocy
23 lut 01:10
Chciekawy: Ciekawostka? https://en.wikipedia.org/wiki/Langleys_Adventitious_Angles
23 lut 07:39
chichi:
@
Mila nie wiem czy widziałaś wywody Pana M. ale wydaje mi się, że kiedyś z Tobą
rozmawiałem nt. tw. Cevy w wersji trygonometrycznej, bo z wykorzystaniem trygonometrii Pan M.
"dał radę" − choć to tylko i wyłącznie jego zdanie i jak rzekł było to "piękne rozwiązanie"
natomiast tw. o którym wspomniałem szybko przynosi rozwiązanie
P.S. zadanie to dziś dałem uczestnikom kółka z geometrii elementarnej dla uczestników OMJ,
które prowadzę i znaleźli 3 inne rozwiązania syntetyczne, nikt nie ważył się porwać na rozw.
Pana M.
23 lut 21:03
Mila:
chichi widziałam, dobrze, że ktoś usunął. (Może
Eta , bo widzę, że jest na forum)
Absolutnie bez trygonometrii.
Tw. Cevy w wersji trygonometrycznej w niektórych przypadkach przydaje się.
Wszystko zależy od tego jak te kąty są podzielone.
Próbowałam to w różnych zadaniach i czasem trzeba było mieć w pamięci różne
zależności trygonometryczne, to szybko się liczyło.
Gratuluję ambitnych uczniów
24 lut 00:01
chichi:
a ja gratuluję Wam wkład w kształcenie tych młodych, którzy mówili, że dużo wiedzy czerpali z
internetu (jak to samouki) wymieniono mi takie nicki z forum:
−Mila
−Eta
−PW
−Bogdan
2 ostatnich (Panów jak domniemywam nie znam, ale miło słyszeć), pozdrawiam i czujcie się
docenieni
24 lut 00:18
Mila:
Dziękuję
chichi Pozdrów naszych byłych forumowiczów.
24 lut 00:48
Bogdan:
Dziękuję
chichi, pojawiam się tutaj od wielu lat, w ostatnim czasie pod różnymi imionami,
ostatnio byłem "Likwidatorem" i taxi i ixi i pixi i inne. Z wielka przyjemnością czytam
Twoje wpisy.
Eta natychmiast rozpoznaje moje wpisy i wtedy wysyła mi uśmieszki
,
ale widzę, że nie tylko
Eta rozpoznaje starych bywalców tego pożytecznego Forum.
Pozdrawiam serdecznie
24 lut 01:04
Mila:
24 lut 14:38
Mariusz:
Syntetyczne rozwiązania chichi są piękne. Zazdrościsz?
Jedyne czego mogę zazdrościć to Jakubowi że nie mam jego uprawnień
22 maj 13:21
chichi:
ty masz gościu obsesje na moim punkcie? wykopujesz jakieś posty sprzed 15 miesięcy i się tu
faflunisz dziadku, w japę dawno nie dostałeś chyba
22 maj 14:14
