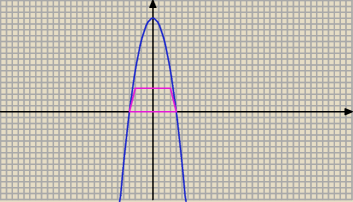
Dana jest funkcja f(x)= 16 - x^2 rega: Dana jest funkcja f(x)= 16 − x² . W parabolę będącą wykresem funkcji f wpisano trapez równoramienny w taki sposób, że dłuższa podstawa trapezu leży na osi OX , a jej końce to miejsca zerowe funkcji f . Końce krótszej podstawy leżą na paraboli i znajdują się powyżej osi OX (zob. rysunek). Wykaż, że pole każdego takiego trapezu jest mniejsze od 76. Wychodzą mi liczby nie z tej ziemi, proszę o pomoc,

. : Jaki poziom nauczania?

rega: Bardzo niski tzw. liceum

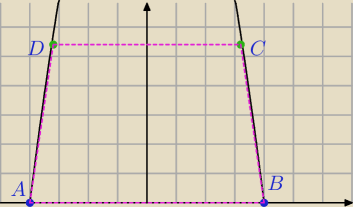wredulus_pospolitus: 1) zauważmy, że dłuższa podstawa ma stałą długość i wynosi ona 8 2) długość krótszej podstawy oraz wysokość trapezu wyznaczamy w zależności od (x) C(x , 16−x²) −−−> −−−> długość krótszej podstawa = 2x −−−> h = 16−x²

	8+2x
Ptrapezu(x) =		*(16−x2) = (4+x)*(16−x2) ; x∊(0;4)
	2

P'(x) = ..... i szukasz maksimum

rega: Tak, to wszystko mam. Jednak maksimum wychodzi mi U[4}{3} ,co daje mi strasznie brzydkie wyniki.

wynikowy: A to wynik ma być ładny? Wynik to wynik. Jeśli wszystko po drodze jest dobrze, to znaczy, że wynik też jest dobry.

. : A od kiedy wynik

	16		128		2048		2052
P ≤		*		=		<		= 76
	3		9		27		27

To jest 'strasznie brzydkie liczby'

. : Wystarczy się pozbyć idiotycznej tendencji do nie zostawiania wyników w postaci nieskracalnych ulamkow.

Min. Edukacji: