Pokaż że równanie |x+2|-|x+7|=-6 nie ma rozwiązań qwerty: Pokaż że równanie |x+2|−|x+7|=−6 nie ma rozwiązań ||x+2|−|x+7||=||x+2|−|−x−7||≤|x+2+(−x−7)|=|−5|=5 ||x+2|−|x+7||≤5, czyli −5 ≤ |2+2|−|x+7| ≤ 5 Dla dowolnej liczby x wyrażenie |x+2|−|x+7| przyjmuje wartości z przedziału [−5, 5], więc równaie |x+2|−|x+7|=−6 jest sprzeczne. Dlaczego w tym przykładzie jest ≤ a nie < skoro według własności wartości bezwzględnej wynika że ||x|−|y||<|x+y|, nie ||x|−|y||≤|x+y|?

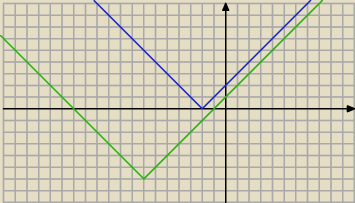ada: f(x)= |x+2| , g(x)= |x+7|−6 f(x)=g(x) x∊∅

qwerty: Nadal nie rozumiem

qwerty: Moje pytanie to czemu jest w tym przykładzie ≤ a nie <

chichi: oczywiście, że w tym twierdzeniu są nierówności nieostre, nie wiem skąd Ty ostre wyczarowałeś

ABC: nie pomyślał o kontrprzykładzie x=0, y=0 nauczanie leży w tym kraju