w. bezwzg.
xhxh: x2 − 3IxI −4 ≤ 0
wyznaczyłam przedziały (−∞, 0) i [0, +∞)
z pierwszego przedziału wyszło mi x= [−4, 1]
z drugiego x= [−1, 4]
z części wspólnej obliczyłam x= [−1, 1] a w odpowiedziach jest [−4, 4]. Pomoże mi ktoś?
12 lut 17:45
xhxh: podejrzewam że to kwestia tego, że w niektórych przypadkach wyznacza się część wspólną, a w
innych sumę. Jeśli tak jest mógłby mi ktoś wytłumaczyć od czego to zależy?
12 lut 18:12
Mila:
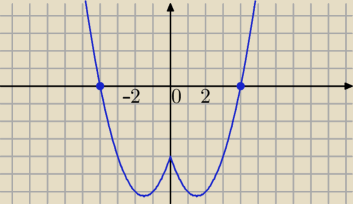
Wspomaganie graficzne.
1)
x
2−3x−4=0
x=−1 lub x=4
Stąd
x
1=−4, x
2=4
2)
x
2−3|x|−4≤0
−4≤x≤4
12 lut 18:23
chichi:
polecam podstawienie t = |x|

12 lut 18:32
Mila:
Algebraicznie przy podstawieniu 18:32.

12 lut 18:47
xhxh: nie za bardzo wiem o co chodzi z tym podstawieniem. Nie wiem kiedy wyznaczyć część wspólną, a
kiedy sumę przedziałów. Np. w tym przykładzie:
x2− 7IxI+ 10 ≤ 0
w jednym źródle pisze, że poprawny wynik to x należy do ∅ (czyli została wyznaczona część
wspólna), a w innym źródle pisze że x należy do [−5, −2] ∪ [2,5] (czyli wyznaczono sumę)
może ktoś potrafi mi wytłumaczyć skąd mam wiedzieć kiedy wyznaczyć sumę przedziałów a kiedy
część wspólną?
12 lut 18:54
xhxh: w tym przykładzie wyszły takie przedziały:
1) x= −2
x= −5
czyli przedział x należy do [−5, −2]
2) x= 2
x= 5
czyli przedział x należy do [5, 2]
12 lut 18:56
xhxh:
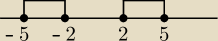
12 lut 19:00
 Wspomaganie graficzne.
1)
x2−3x−4=0
x=−1 lub x=4
Wspomaganie graficzne.
1)
x2−3x−4=0
x=−1 lub x=4