w. bezwzględna
xhxh: cześć, mogę prosić o pomoc z równaniem z wartością bezwzględną?
I3x−6I + Ix−3I = 30
rozpisałam sobie takie przedziały:
(−∞, 2)
[2,3)
[3, +∞)
Nie wiem jak wybrać liczbę, która należy do tego przedziału [2,3). Jak wybiorę 2 to wartość
bezwzględna wychodzi na 0 i nie wiem czy wtedy zmienić znaki, czy nie. Może ktoś pomóc?
12 lut 15:45
mat: nie wybieraj granicznych wartośi tylko coś ze środka przedziału
12 lut 15:53
mat: dla [2,3) np 2.5 −−> w pierwszej wattości bezwzlgednej jest ujemny wynik, w drugiej tez więc
zmieniamy znaki
−(3x−6) + (−(x−3)) = 30
−3x+6 − x + 3 = 30 itd
12 lut 15:54
mat: pierwsza jest dodatnia**
(3x−6) + ..
12 lut 15:55
xhxh: wszystko jasne, dzięki za pomoc

12 lut 15:55
Mila:
I3x−6I + Ix−3I = 30⇔
3|x−2|+|x−3|=30
1) dla x<2 obydwa wyrażenia : x−2 i x−3 przyjmują wartości ujemne
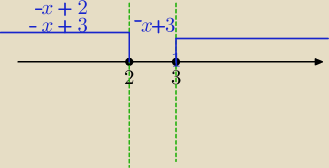
|x−2|=−x+2 , |x−3|=−x+3
( na osi zaznaczam tylko zmiany )
Masz równanie:
3(−x+2)+(−x+3)=30
rozwiąż
2) Dla x∊<2,3) mamy x−2≥0 a x−3<0
|x−2|=x−2, |x−3|=−x+3
Równanie:
3(x−2)+(−x+3)=30
3x−6−x+3=30
2x=33
3) dla x≥3 obydwa wyrażenia : x−2 i x−3 przyjmują nieujemne
Równanie
3(x−2)+x−3=30
dokończ.
12 lut 16:05

 I3x−6I + Ix−3I = 30⇔
3|x−2|+|x−3|=30
1) dla x<2 obydwa wyrażenia : x−2 i x−3 przyjmują wartości ujemne
|x−2|=−x+2 , |x−3|=−x+3
( na osi zaznaczam tylko zmiany )
Masz równanie:
3(−x+2)+(−x+3)=30
rozwiąż
2) Dla x∊<2,3) mamy x−2≥0 a x−3<0
|x−2|=x−2, |x−3|=−x+3
Równanie:
3(x−2)+(−x+3)=30
3x−6−x+3=30
2x=33
I3x−6I + Ix−3I = 30⇔
3|x−2|+|x−3|=30
1) dla x<2 obydwa wyrażenia : x−2 i x−3 przyjmują wartości ujemne
|x−2|=−x+2 , |x−3|=−x+3
( na osi zaznaczam tylko zmiany )
Masz równanie:
3(−x+2)+(−x+3)=30
rozwiąż
2) Dla x∊<2,3) mamy x−2≥0 a x−3<0
|x−2|=x−2, |x−3|=−x+3
Równanie:
3(x−2)+(−x+3)=30
3x−6−x+3=30
2x=33