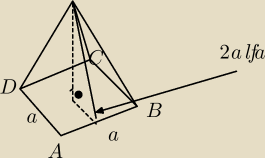
 dany jest ostroslup prawidlowy czworokatny abcds o podstawie abcd i polu powierchni calkowitej
rownym S.
miara kata dwusciemnnego miedzy podstawa a plaszczyzna boczna wynosi 2α. Objetosc tego
ostroslupa
jest rowna k √S3 cos(2α) * ( sin(α) ) / (cos2 (α) ) gdzie k jest stalym wspolczynnikeim.
OPblicz k
l
wyszlo mi ze
h bocznej sciany = a / (cos2α)
H = 1/2 * a * (sin2α / cos2α)
a2 = (Scos2α) / (cos2α + 1)
i licze objetosc
V = 1/3 * (Scos2α) / (cos2α + 1) * 1/2 * √(Scos2α) / (cos2α + 1) * (sin2α / cos2α)
ale nie wiem jak to dalej ogarnac i przeeszktalcic zeby to k wyszlo
dany jest ostroslup prawidlowy czworokatny abcds o podstawie abcd i polu powierchni calkowitej
rownym S.
miara kata dwusciemnnego miedzy podstawa a plaszczyzna boczna wynosi 2α. Objetosc tego
ostroslupa
jest rowna k √S3 cos(2α) * ( sin(α) ) / (cos2 (α) ) gdzie k jest stalym wspolczynnikeim.
OPblicz k
l
wyszlo mi ze
h bocznej sciany = a / (cos2α)
H = 1/2 * a * (sin2α / cos2α)
a2 = (Scos2α) / (cos2α + 1)
i licze objetosc
V = 1/3 * (Scos2α) / (cos2α + 1) * 1/2 * √(Scos2α) / (cos2α + 1) * (sin2α / cos2α)
ale nie wiem jak to dalej ogarnac i przeeszktalcic zeby to k wyszlo
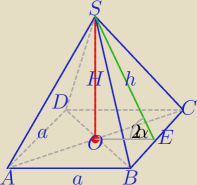 Pc=S
Pc=S
| √S3cos(2α)*sinα | ||
V=k* | ||
| cos2α |
| sinα | ||
V=k*√S3cos(2α)* | ||
| cos2α |
| √2 | ||
k= | ||
| 6 |
| 12a | ||
cos(2α)= | ||
| h |
| a | ||
h= | ||
| 2cos(2α) |
| H | ||
tg(2α)= | ||
| 12a |
| 1 | ||
H= | a*tg(2α) | |
| 2 |
| a | a2 | |||
S=a2+2*a* | =a2+ | |||
| 2cos(2α) | cos2α |
| 1 | ||
S=a2*(1+ | )⇔ | |
| cos(2α) |
| cos(2α)+1 | ||
S=a2* | ||
| cos(2α) |
| S*cos(2α) | √S*cos(2α) | |||
a2= | ⇔a= | |||
| 2cos2(α) | √2cos(α) |
| 1 | √S*cos(2α) | 2sinα*cosα | ||||
H= | * | * | ||||
| 2 | √2cos(α) | cos(2α) |
| sin(α) | ||
H=√S cos(2α)* | ||
| √2cos(2α) |
| 1 | S*cos(2α) | sin(α) | ||||
4) V= | * | *√S cos(2α)* | = | |||
| 3 | 2cos2(α) | √2cos(2α) |
| S*sinα*√S cos(2α) | sinα | |||
= | =√S3cos(2α)* | |||
| 6√2cos2(α) | 6√2*cos2α |
| sinα | sinα | |||
k*√S3cos(2α)* | =√S3cos(2α)* | |||
| cos2α | 6√2cos2α |
| 1 | ||
k= | ||
| 6√2 |
| √2 | ||
k= | ||
| 12 |
 Dzięki za sprawdzenie.
Dzięki za sprawdzenie.