Piramida cheopsa Algorytmika : Pytanie szybkie. Mam zadanie do rozwiązania z algorytmiki. Chciałbym policzyć ile średnio zużyto materialu budowlanego do zbudowania tej piramidy. Cała piramida składa się z 2,5mln kamieni, który każdy średnio waży 2,5t, największy kamień tej piramidy waży 20t. Jak to policzyć. Przepraszam za trudność ale policzyłem tylko mam wątpliwość co do wyniku. Mógłby mnie ktoś poratować wsparciem?

wredulus_pospolitus: skoro ŚREDNIO jeden kamień waży 2.5t a kamieni masz 2.5mln ... to one ważą łącznie: 2.5t * 2.5*10⁶ = ...

wredulus_pospolitus: informacja o tym ile waży największy kamień jest tu nam całkowicie zbędna

Algorytmika : Też się zastanawiałem po co waga najcięższego ale nie ja jestem autorem zadania. Dzięki. Czy mógłbym prosić o pomoc w jeszcze 2 zadaniach? 1.przyjmij że piramida składa się z 2.5mln kamiennych bloków. Załóż również że budowano ją przez 20 lat pracując każdego dnia 14 godzin na dobę. Przyjmując że bloki trafiały na swoje miejsce w równych odstępach czasu, oblicz jak często (czyli co ile minut) musiano je ustawiać na swoim miejscu. 2. Przyjmij dla ułatwienia że piramidę Cheopsa zbudowano z jednakowych bloków o wysokości 2m i wymiarach podstawy 3x3m. Z ilu takich bloków musiałaby się ona składać? Co ile minut taki blok musiałby trafiać na swoje miejsce gdyby wznoszono ją po 14 godzin dziennie przez 20 lat. Wskazówka: podziel całą piramidę na warstwy o wysokości równej 2m i oblicz ile bloków o rozmiarach 3x3m znajdzie się w każdej warstwie. Następnie zsumuj te liczby. Będę wdzięczny za pomoc. Oczywiście nie będę bezmyślnie czekał na pomoc. Sam też coś będę się starał rozwiązywać.

wredulus_pospolitus: 1) 20*365*14*60 = .... min pracy dzielisz i gotowe 2) Trudno powiedzieć, bo nie wiem ile wysokości i jaką podstawę ma ta piramida

wredulus_pospolitus: Jak również pod jakim kątem jest zbudowana

Algorytmika : Jej wysokość to 150m, a wszystkie boki podstawy to 230m

Algorytmika : Boki są niemal dokładnie zorientowane według stron świata− odchylenia nie przekraczają 5 min, a zatem krawędzie podstawy tworzą w narożnikach niemal idealne kąty proste.

Algorytmika : Ja mam takie pytanie odnośnie tej wskazówki do zadania drugiego. Chodzi o to żeby całą piramidę podzielić na warstwy o wysokości równej 2m. Cała piramida ma 150m wysokości , a każdy blok ma 2m wysokości. Więc dzielę 150:2=75. I obliczyć ile bloków o wymiarach 3m na 3m znajdzie się w każdej warstwie i zsumować te liczby. No to podzieliłem wysokość całej piramidy(150) przez wysokość każdego bloku(2) i wyszło 75. Wychodzi że trzeba podzielić ta piramidę na 75 równych 2m warstw. Natomiast jak obliczyć żeby sprawdzić ile w każdej z tych warstw o wysokości 2m można umieścić tych bloków o wymiarach 3 na 3m. Jak to zapisać. Chciałem to zrobić za pomocą nierówności ale nie bardzo wiem jakbym miał zapisać jako 3 na 3m =75. Jak to obliczyć?

Algorytmika : Chyba że wiedząc że całą podstawą tych bloków ma 3 na 3 a więc jest to kwadrat to może można to uprościć i zapisać tak: 3x=75/:3 −> x=25

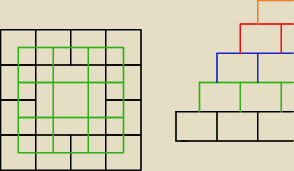
wredulus_pospolitus: Jest wiele pytań: 1) Czy zakładamy, że piramida wewnątrz jest pusta czy pełna bloków 2) POD JAKIM KĄTEM są ściany boczne −> tu co prawda, ze względu na to że bloki mają stałe wymiary można łatwo zauważyć, że tylko jeden układ da nam zawsze całkowitą liczbę bloków na każdym poziomie −−− pokazane na rysunku −−− rzut z góry oraz z boku

wredulus_pospolitus: Jednak czy każdy poziom (poza pierwszym i ostatnim) będzie tylko 'framugą' czy też tak jak podstawa całkowicie wypełniona blokami kamiennymi −−− tego nie wiadomo

Algorytmika: Z tymi danymi to zadanie jest niewykonalne?

wredulus_pospolitus: nie wiem ... przyjmij na początek że będzie w całości zapełniona. Zauważ wtedy, że każdy poziom (zaczynając od czubka = 1 klocek) będzie dokładnie n² bloków Taka jedna uwaga −−− boki podstawy nie mogą mieć 230m Będą miały 225m.

Algorytmika: Czemu twierdzisz że będzie "Zauważ wtedy, że każdy poziom (zaczynając od czubka = 1 klocek) będzie dokładnie n2 bloków ". Jak do tego doszedłeś? "Taka jedna uwaga −−− boki podstawy nie mogą mieć 230m Będą miały 225m." Mają ok.230m

Thomas: Why do you state that each level, beginning at the top where there is one block, will have exactly n2 blocks? Describe your journey there." Just one thing: the base's sides cannot be 230 metres long. They'll be 225 metres." They are roughly 230 metres.https://techemirate.com/com-sec-android-daemonapp/