styczna sowa: funkcja f jes okreslona wzorem x² + (8/x) − 7 wyznacz rowanie stycznej do wykresu funckji f rownoleglej do prostej y = 2x +1 i robilem tak ze policzylem pochodna f i mi wyszlo 2x − (8/x²) =0 i mi wyszlo ze x = ³√4 i teraz policzylem jaka to wartosc dla funkcji f i podstawilem wszystko pod wzor y = a (x − x0) + f(x0) czy to ma wszystko sens?

mat: nonsens

sowa: a jak nalezy to zrobic

Jolanta: pochodna z ułamka

	pochodna licznika*mianownik−licznik*pochodna mianownika
=
	mianownik 2

mat: styczna ma równanie: y= f^'(x_o)(x−x_o)+y_o , P(x_o,y_o) −− punkt styczności f^'(x_o)=2 −− współczynnik kierunkowy stycznej równoległej do prostej y=2x+1

	8
f'(x)= 2x−		, x≠0
	x2

f^'(x_o) =2

	8
2xo−		=2
	xo2

x_o³−x_o²−4=0 (x_o−2)(x_o²+x_o+2)=0 x_o= 2, więc y_o= f(2)= 4+4−7 =1 P(2,1) styczna ma równanie y= 2(x−2)+1 y= 2x−3

sowa: ale co z tego nie mozna z tego a/x = − a/x² ? Chodzi o to ze zle policzylem pochodna i jest zle czy caly etap i pomysl jest zly i trzeba calkiem inaczej?

sowa: ale skąd ci wyszlo x0 = 2 skoro tej pochodnej f'(x) punkty zerowy to pierwiastek trzeciego stopnia z czterech

mat: https://matematykaszkolna.pl/strona/4334.html doucz się tu od p. Jakuba

sowa: no ale nie mozna tego robic tak ze liczysz pierwiastek pochodnej i podstawiasz?

Mila:

	8
f(x)=x2 +		− 7, x≠0
	x

	8
f'(x)=2x−
	x2

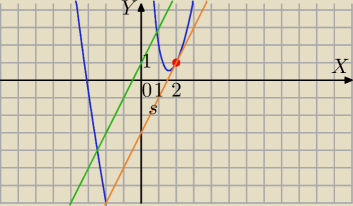
Szukamy punktu styczności (x₀,y₀) s: y=2(x−2)+y₀ f'(x₀)=2

	8
2x0−		=2
	x02

x₀=2 , y₀=f(2)=1 s: y=2x−4+1 y=2x−3 ======

sowa: ale czy to f'(x0) nie powinno dac sie wyliczyc liczac miejsce zerowe pochodnej?

sowa: ale czy to f'(x0) nie powinno dac sie wyliczyc liczac miejsce zerowe pochodnej?

mat: U Mili to samo, tylko kolorowo

Jolanta: Pochodna policzyłes dobrze Dawno to liczyłam ale pamiętam,że współczynnik kierunkowy prostej równy jest pochodnej w punkcie stycznosci

Mila: mat gdy zaczęłam pisać nie było Twojego wpisu (odrywali mnie od pisania i tak mi zeszło).