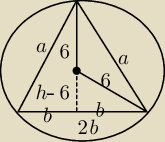
 rozwazamy trojkaty rownoramienne na ktorych opisano okrag o promieniu 6. wyznacz dlugosc bokow
tego trojkata kotry ma najwieksze pole. Oblicz to pole
i z pitagorasa uzaleznilem sobie funkcje pola od H
(h−6)2 + b2 = 62
b=√12h − h2
P(H) = (√12H − H2 * H )
czy dobrze? Czy ktos moze pomoc dalej bo obstawiam ze trzeba obliczxyc pochodna ale tu sie
zaczynaja problemy. Czy ktos moze pomoc pokazac dalsze rozwiazanie jesli to jest dobre i podac
wynik?>
rozwazamy trojkaty rownoramienne na ktorych opisano okrag o promieniu 6. wyznacz dlugosc bokow
tego trojkata kotry ma najwieksze pole. Oblicz to pole
i z pitagorasa uzaleznilem sobie funkcje pola od H
(h−6)2 + b2 = 62
b=√12h − h2
P(H) = (√12H − H2 * H )
czy dobrze? Czy ktos moze pomoc dalej bo obstawiam ze trzeba obliczxyc pochodna ale tu sie
zaczynaja problemy. Czy ktos moze pomoc pokazac dalsze rozwiazanie jesli to jest dobre i podac
wynik?>
| 1 | ||
P'(H) = | *(12 − 2H)*H + √12H−H2 = | |
| 2√12H−H2 |
| 6H − H2 + (12H − H2) | ||
= | ||
| √12H − H2 |
 )
)