Ostrosłup sprawdzenie Halinka: Dany jest ostrosłup prawidłowy czworokątny ABCDS. Pole podstawy ABCD jest równe 64, a tagens kata nachylenia wysokości sciany bocznej do paszczyzny podstawy wynosi 3/4. Oblicz pole powierzchni bocznej tego ostrosłupa. Pytanie? czy ten ostrosłup ma w podstawie kwadrat i a mogę policzyć z P=a² ten trójkąt utworzony z wysokości ściany bocznej i wysokości ostrosłupa da mi tgα=^H_x z czego H=3/4x I co dalej ?

Halinka: Uprzedzę pytania −rysunek mam

Jolanta: Tak słowo prawidłowy oznacza w podstawie figure o równych bokach jeżeli x=1/2 a to dobrze myslisz

Jolanta: 3/4=tg. tg=H/4 3/4=H/4

Jolanta: H ostrosłupa ,1/2 a i h trójkąta tworzą trójkąt prostokątny czyli Pitagoras się kłania

Halinka: czyli moge przyjąc ,że bok a =8

Jolanta: Musi=8 skoro P=64 =a*a

Halinka: dzieki Jolu

Jolanta: Korzystam z telefonu inie umiem tutaj pisac Piszesz wzór na pole piwerwiastkujesz obustronniei wychodzi a=8

Halinka: to juz łatwiej mi bedzie, chciałam sie upewnic

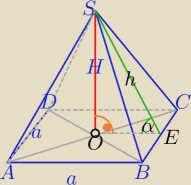
Mila: 1) P_□=a² a²=64 a=8 2)W ΔSOE:

	H		3		H
tgα=		, ⇔		=		⇔H=3
	|OE|		4		4

ΔSOE− Δegipski (3,4,5) h=5 dalej sama