pierwiastki w przedziale asia: wyznacz wszystkie wartosci parametru k dla ktorych dwa rozne pierwiastki rownania x² + 2(k−4)x +16 = 0 należą do przedziału (−5, 2)

s.o.s.:

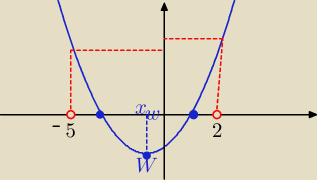
	⎧	Δ>0
	⎜	f(−5)>0
	⎨	f(2)>0
	⎩	−5<xw<2

asia: a moze ktos stwierdzic jaka jest odpowiedz, koncowy przedzial? Bo mi wyszlo delta (−∞ ; 0) U (8; +∞) f(−5) > 0 k< 8,1 f(2) >0 k> −1 −5<p<2 k ∊ (2; 9) odp? (8: 8,1)

wredulus_pospolitus: x² + 2(k−4)x +16 = 0 (x−(4−k))² −(k²−8k) = 0 stąd wiemy, że: 1. Δ > 0 ⇔ k²−8k > 0 −−−> więc także dobrze 2. f(−5) = (k−9)² − k(k−8) = −10k + 81 −−−> k> 8.1 3. f(2) = (k−2)² − k(k−8) = 4k + 4 −−−> k>−1 4. x_wierzchołka = 4−k −−−> 4−k ∊ (−5;2) −−−> k∊(2;9)

asia: dlaczego k> 8.1? −10k + 81 >0 81> 10k 8,1 > k

asia: bo mi sie to nie zgadza