trapez juliank: Dany jest trapez ABCD o podstawach AB i CD. Przekątne AC i BD mają długości równe 5 cm i 3 cm. Niech E będzie środkiem odcinka CD, a F środkiem odcinka AB, wtedy odcinek EF będzie miał długość 2 cm. Oblicz pole ABCD

M:

N :

messi: β = 180^o − α, cos(180^o − α) = −cosα, a + b = c, |AB| = 2a, |AK| = |KG| = a+b = c

	1
Pole trapezu ABCD: P1 =		(2a + 2b)h = (a + b)h = ch.
	2

	1
Pole trójkąta AGC: P2 =		(2a + 2b)h = (a + b)h = ch = P1
	2

Teraz wystarczy zastosować twierdzenie cosinusów dla trójkątów AKC i KGC

kibic: I jaki masz wynik piłkarzu?

arbiter : P=6

Iryt:

chichi: solilokwium

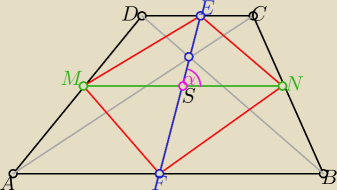Eta: Inny sposób : Czworokąt FNEM jest równoległobokiem o bokach :

	5		3
|ME|=|FN|=		i |FM|=|NE|=		i FE|=e=2
	2		2

	a+b
||MN|=s=
	2

	1
P(trapezu)= 2P(FNEM) = 2*		*s*e*sinα
	2

P_t= 2s*sinα w równoległoboku zachodzi :

	9		25
s2+e2=2|MF|2+2|FN|2 ⇒ s2+4=		+		⇒ s=√13
	2		2

z tw. cosinusów w ΔNSE :

	13   9   1+ −   4   4		2
cosα=		=..=
	√13   2*1*   2		√13

	3
to sinα=
	√13

zatem pole trapezu :

	3
P=2√31*
	√13

P= 6 ======

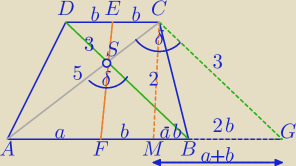Mila: Dołączę się . CM||EF CM=2 − środkowa w ΔACG 1) Tw. Stewarta ( albo tw. cosinusów) dla środkowej. 5²+3²=2*(2²+(a+b)²) (a+b)²=13 (a+b)=√13 2) Tw. cosinusów w ΔAGC (2√13)²=5²+3²−2*3*5 cosδ

	3		4
cosδ=−		, sinδ=
	5		5

ΔASB∼ΔACG 3)

	1		1		4
PABCD=		*5*3*sinδ=		*5*3*
	2		2		5

P_ABCD=6 ========= Pozdrowienia dla autorów rozwiązań.