W trapezie ABCD o podstawach AB=9 i CD=4
Monika: Bardzo proszę o pomoc w rozwiązaniu zad. kl. 3 liceum.
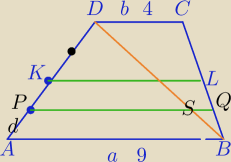
W trapezie ABCD o podstawach AB=9 i CD=4 i AD>BC, punkt P podzielił ramię AD w stosunku 1:3.
Przez punkt P poprowadzono równoległą do AB, która przecina ramię BC w punkcie Q.
Oblicz dług. odcinków PS i SQ, jeśli S jest punktem przecięcia przekątnej DB trapezu z
odcinkiem PQ.
1 lut 17:15
Mila:
| | PD | | 3 | |
1) ΔPSD∼ΔABD w skali k= |
| = |
| |
| | AD | | 4 | |
f=|PS|
Licz dalej sama
1 lut 18:16
Monika: Dziękuję Ci Mila za piękny rysunek.
No tak, nie zauważyłam, że pomocny będzie ten KL, bo wtedy wyjdzie jako średnia arytmetyczna
ten odcinek PQ.
PQ mam = 7,75.
Ale z jakiej proporcji − Talesa wyliczyć teraz PS?
Zupełnie nie mam na to pomysłu. Proszę o wskazówkę.
1 lut 18:39
Mila:
|PS| z podobieństwa Δ z (1) punktu − pierwsza linijka.
1 lut 18:47
Monika: Aha, dobrze.
To proszę Cię o sprawdzenie, czy szłam dobrą drogą.
Oznaczyłam szukane PS=y i wtedy SQ=7,75 − y
I dalej tak, jak mi podpowiedziałaś:
PD / PS = AD / AB
więc 3/y = 4 /9 i stąd mam y= 6,75
Potem już łatwo, bo SQ = 7,75 − 6,75 = 1.
1 lut 19:05
Mila:
Wynik dobry.
| | 3 | |
Można krócej− |PS|= |
| *9 |
| | 4 | |
1 lut 19:56
Monika: Bardzo Ci Mila dziękuję za ogromną pomoc. Ten KL był ważny

1 lut 20:00

