trójkąt rozwartokątny maniek: W trójkącie rozwartokątnym ABC o kącie rozwartym przy wierzchołku A poprowadzono wysokości BD i CE . Następnie wysokości te przedłużono do przecięcia w punkcie F. Wykaż, że |<AFB| = |<AED|.

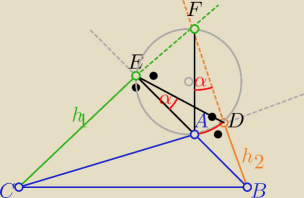
s.o.s.: Na czworokącie ADFE da się opisać okrąg bo |∡ADE|+ ∡AEF|= 180^o zatem kąty α mają równe miary bo są wpisane w ten okrąg i oparte na tym samym łuku AD co kończy dowód |∡AFB|= |∡AED|=α

s.o.s.: poprawiam zapis ..... bo |∡ADF|+|∡AEF|=180^o