Funkcja "na" Aruseq: Wskazać przykład funkcji spełniającej dany warunek lub wskazać, że taka funkcja istnieje: f: (0, 1]−>[0,1] ciągła i "na" I tutaj nie wiem. Na logikę skoro ma być to funkcja "na" to powinienem skupiać się tylko na tym przedziale [0, 1], natomiast skoro mam w ogóle wskazać taką funkcję, to ona siłą rzeczy będzie funkcją "na", bo musi przyjmować te wartości z przedziału [0, 1]. Nie wiem, czy w moim myśleniu jest jakiś błąd?

Aruseq: Chociaż w innym podpunkcie jest ten sam przedział i ma być ciągła i różnowartościowa. Czyli raczej ma być funkcją "na" na całym R

ABC: ciągła bijekcja między tymi zbiorami nie jest możliwa bo ciągły obraz zbioru domkniętego musi być domknięty natomiast ciągłą która nie jest różnowartościowa złożysz używając sinusa

Aruseq: Chyba nie do końca zrozumiałem I też średnio widzę w tym odpowiedź na moje pytanie. Może napisze jakie dałbym odpowiedzi do obu tych przykładów i wtedy ewentualnie łatwiej powinienem wyhaczyć ewentualne błędy. a) f: (0, 1]−>[0,1] ciągła i "na"

	1
I tutaj mam właśnie największy dylemat. Z jednej strony funkcja y=4(x−		)2 mi pasuje, bo
	2

wydaje mi się że spełnia te wszystkie warunki. Natomiast w kolejnym podpunkcie: b) f: (0, 1]−>[0,1] ciągła i różnowartościowa przez słowo różnowartościowa mam wątpliwości, czy ta funkcja z podpunktu a) ma nie być funkcją "na" w liczbach rzeczywistych. Wtedy ta moja odpowiedź nie pasuje, ponieważ nie możemy mówić o funkcji różnowartościowej jak mamy tylko przedział (0, 1]. Natomiast w podpunkcie b dałbym na przykład y=sin(πx)

Aruseq: Ma to wszystko sens?

Fałszywy 6-latek:

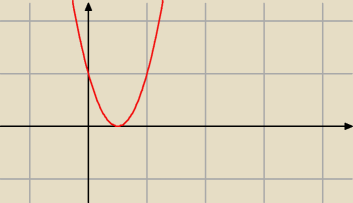
	1
ta funkcja twoja 4(x−		) jest też dobra
	2

ale ciągłej i różnowartościowej nie można zbudować z powodów topologicznych

Aruseq: A czemu? Ten mój przykład nie jest okej?

chichi: no a co jest ona wg Ciebie różnowartościowa?

chichi: "nie pasuje, ponieważ nie możemy mówić o funkcji różnowartościowej jak mamy tylko przedział (0, 1]." ze niby co? skąd te dziwne wnioski?

Aruseq: Racja, ja cały czas z jakiegoś powodu myślałem o funkcji nieparzystej i stąd te wszystkie wnioski. Dzięki