cięciwa Mark: Skonstruowano półkole, którego średnicą jest odcinek AD=3cm. Na łuku tego półkola zaznaczono dwa punkty B i C tak, że AB=BC=1 cm. Znajdź długość cięciwy CD.

wredulus_pospolitus:

	1		4
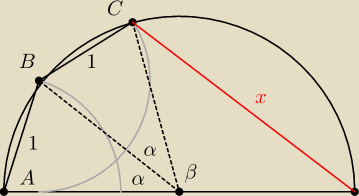
1 = 2.25 + 2.25 − 5cosα −−> 1 = 5(1−cosα) −−−> cosa = 1 −		=
	5		5

	16		7
−−> cos(2α) = 2*		− 1 =
	25		25

	32
x2 = 2.25 + 2.25 − 5cosβ = 5(1−cosβ) = 5(1−cos(180 − 2α)) = 5(1+cos(2α)) = 5*		=
	25

	160		4
=		−−> x =		√10
	25		5

ite: a nie 1 = 2.25 + 2.25 − 4,5cosα ?

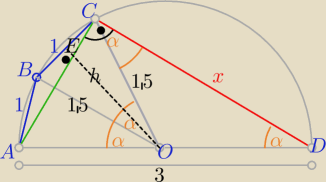s.o.s.: W ΔADC : x= 3*cosα W ΔOBE : h=...... = √2

	√2		1		4√2
PΔOBC=		i PΔOBC=		*1,5*1,5*sinα ⇒ sinα=
	2		2		9

	7
to cosα= √1−sin2α = ......... =
	9

	7
x= 3*
	9

	1
x= 2
	3

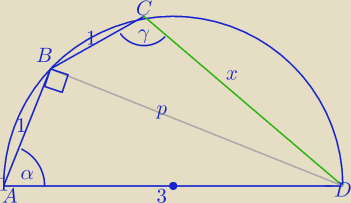Mila: II sposób 1) W ΔABD:

	1
cosα=
	3

Z tw.Pitagorasa p²=8 2) W ΔBCD: γ=180−α p²=1+x²−2x*cos(180−α)

	1
8=1+x2+2x*		, x>0
	3

	7
x=
	3

====