Katy w trójkacie Justyna: Dany jest Δ równoramienny ABC, w którym AC=BC=8 oraz AC=4* AB. Odcinek AD ,gdzie D jest punktem boku BC jest zawarty w dwusiecznej kąta CAB. Należy obliczyć cosinus najmniejszego kąta w trójkącie ABC. Prosze o podpowiedz. czy kat , o ktory pytaja jest przy wierzchołkuC? Czy jest to kat podzielony na dwa przez dwusieczna?

chichi: tak, dwusieczną kąta nazywamy półprostą wychodzącą z wierzchołka tego kąta i dzielącą tenże kąt na dwa kąty jednakowej miary

Hala: Czyli jak dobrze rozumiem to będzie jeden z tych dwóch kątów?

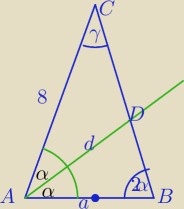
Mila: Dwusieczna kąta CAB − kąt A został podzielony

chichi: "Czyli jak dobrze rozumiem to będzie jeden z tych dwóch kątów?" masz obliczyć cosinus najmniejszego kąta w ΔABC, czyli kąta cos(γ) z @Mila rysunku

Misia: Jak policzyc ten kat gamma? wiem,ze wszystkie kąty to 180 mam 4 alfa ale nie znam ich miary

Mila: Np. Z twierdzenia cosinusów.

Jolanta: AC=4*AB AB=2 z tw cosinusów 2²=8²+8²−2*8*8cosγ 4=64+64−128cosγ 128cosγ=124

	31
cosγ=		=0,96875
	32