planimetria - dowód Alaias: W trójkącie prostokątnym o przyprostokątnych a i b z wierzchołka kąta prostego poprowadzono wysokość h i dwusieczną, d oznacza odcinek dwusiecznej zawarty w tym trójkącie. Wykaż, że h²/d²=(a+b)²/2(a²+b²).

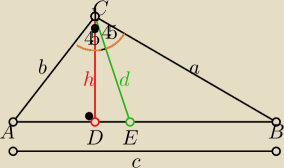
Eta: 1/ a²+b²=c²

	a2b2		c2h2		a2b2		a2b2
2/ (PΔABC)2 =		=		⇒ h2=		=
	4		4		c2		a2+b2

	bd		ad
PΔABC = PΔAEC+PΔBEC =		*sin45o +		*sin45o
	2		2

	√2
ab= d		(a+b)
	2

	d2		2a2b2
to a2b2=		(a+b)2 ⇒ d2=
	2		(a+b)2

i mamy ............ tezę

h2		(a+b)2
	=
d2		2(a2+b2)

============