proszę o rozwiązanie anna: podstawą ostrosłupa jest kwadrat a spodek wysokości ostrosłupa jest jest jednym z wierzchołków tego kwadratu Suma pól powierzchni dwóch ścian bocznych o większym polu jest dwa razy większa od sumy powierzchni pozostałych ścian bocznych Wiedząc że objętość tego ostrosłupa jest równa 81 √3 oblicz a) długość krawędzi podstawy b) długość najdłuższej krawędzi tego ostrosłupa

anna: ja obliczyłam 81√3 = ¹₃a² *h 243√3 = a² *h nie wiem jak zapisać : Suma pól powierzchni dwóch ścian bocznych o większym polu jest dwa razy większa od sumy powierzchni pozostałych ścian bocznych wiem że dwie ściany są trójkątami prostokątnymi 2*( P₁ + P₂ ) = P₃ +P₄

Jolanta:

	a*H
te dwa trójkąty mniejsze maja P=		*2
	2

	a*√a2+H2
Pozostałe mają przyprostokątne a i √a2+H2 P1=		*2
	2

2*P=P₁

	a*H		a*√a2+H2
2*2*		=2*
	2		2

2H=√a²+H² 4h²=a²+H² 3H²=a²

	a
H=
	√3

	1
V=		a2*H
	3

	1		a
81√3=		a2*
	3		√3

9=a

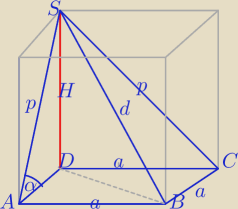
Mila: Dołączam rysunek do obliczeń Jolanty 1) V= 81 √3

	1		1
V=		a2*H⇔		a2*H=81√3
	3		3

a²H=243√3 2)

	p*a		a*H
2(		)=2*[2*		]⇔p*a=2aH
	2		2

p=2H⇔α=30^o

	a
H=
	√3

a=9

anna: dziękuję bardzo