zadanie z parametre,m ricky stonwell: wyznacz wszystkie wartości m lda ktorych trojmian kwadratowy 4x² −2(m+1)x + m ma 2 rozne pierwiastki spelniajace warunki x1 =/= 0 x2 =/= 0 x1 + x2 ≤ 1/x1 + 1/x2 i wiem ze delta > 0 i trzeba to przekształcic ładnie x1 + x2 ≤ 1/x1 + 1/x2 i z tego wychodzi ze m 𝑚 ≠ 1 oraz 𝑚 ∈ (−∞; −1] ∪ (0; 4] ale jak tu zrobić zeby x1 i x2 nie byly zero? jak liczylem po prostu ze wzoru na x1 x2 to mi wyszlo x1 = m/2 oraz x2 = 1/2 czyli co po prostu tego 0 i 1/2? Czy może ktoś sprawdzić?

chichi: gdyby choć jeden z nich byłby 0, to przecież musiałoby x₁x₂ = 0, no to masz x₁x₂ ≠ 0

ricky stonwell: no jeden z nich ale oba maja byc rozne wiec to nie wyklucza przypadku x1 = 0 x2 = np 3

chichi: bzdury piszesz takie, że szok... uzasadnij dlaczego nie wyklucza

Jolanta: 1)Δ>0 m²−2m+1>0 m∊(−∞,1) u(1,∞)

	1		1
2)x1+x2≤		+
	x1		x2

−b		x2+x1
	≤
a		x1*x2

−b		−b		a
	≤		*
a		a		c

−b		b
	+		≤0
a		c

2m+2		−2m−2
	+		≤0
4		m

(m+1)m		(−2m−2)*2
	+		≤0
2m		2m

m2−3m−4
	≤0 m≠0 w liczniku Δ=25 m1=−1 m2=4
2m

co dalej ?

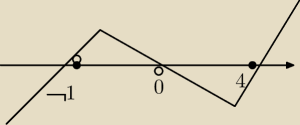
Jolanta: (m+1)(m−4)*2m≤0 m∊(−∞−1> v(0;4> uwzgledniajac poprzednie warunki dla m m∊(−∞−1>v(0;1)v(1;4>