 Oblicz długości wszystkich krawedzi graniastosłupa prawidłowego szesciokątnego przedstawionego
na rysunku ktorego najdłuzsza przekatna ma dlugosc 10 gdy
a= 45 stopni
b= 60 stopni
c= 48 stopni
Oblicz długości wszystkich krawedzi graniastosłupa prawidłowego szesciokątnego przedstawionego
na rysunku ktorego najdłuzsza przekatna ma dlugosc 10 gdy
a= 45 stopni
b= 60 stopni
c= 48 stopni
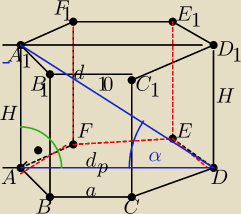 a−krawędz postawy
AD=dp− przekątna podstawy
A1D=d− dłuższa przekatna graniastoslupa
A A1= H− krawędz boczna
a) α=45o
trójkat A1AD to trójkąt prostokątny o kątach 45o, 45o 90o
dp=H
dp√2=10
a−krawędz postawy
AD=dp− przekątna podstawy
A1D=d− dłuższa przekatna graniastoslupa
A A1= H− krawędz boczna
a) α=45o
trójkat A1AD to trójkąt prostokątny o kątach 45o, 45o 90o
dp=H
dp√2=10
| 10 | 10√2 | |||
dp= | = | =5√2 | ||
| √2 | 2 |
| dp | ||
R= | ||
| 2 |
| 5√2 | ||
R= | ||
| 2 |
| 5√2 | ||
a= | ||
| 2 |
| 5√2 | ||
Skr=12* | +6*5√2 | |
| 2 |