przedziały
kasia: |𝑥 − 2| − |𝑥| < 4
i to wiem jak rozwiazac bo sobie rysuje rysunek z przedzialami (szukajac tam gdzie sie zeruje)
i licze w trzech przedzialach
mamy x = 2 i x = 0
wiec
1) (−∞ ; 0)
2) <0 ; 2)
3) <2 ; ∞)
i sobie w tych licze odpowiednio zmieniajac znak pod wart bez i mi dobrze wychodzi
ale inny przykład ||𝑥 +1| − 𝑥| ≤ 2
i tu mam większy problem żeby to narysować i wyznaczyć te przedziały bo ciężko mi z dwoma
wartosciami znaleźć gdzie to sie tam zeruje zeby narysowac
w rozwiazaniach podaja
1)𝑥 ∈ (−∞; −1)
oraz
2)𝑥 ∈ [−1; ∞)
lecz nie bardzo wiem skąd. Proszę o pomoc
6 sty 21:42
ABC: możesz zamienić na podwójną nierówność
−2≤|x+1|−x≤2
i potem rozwiązać dwie nierówności i część wspólną rozwiązań wziąć
6 sty 23:14
kasia: no ale to wychodzi 𝑥 ∈ [−1,5 ; −1) a drugie tożsamość dla 𝑥 ∈ [−1; ∞)
i czesc wspolna jest inna niz rozwiazanie [−1,5 ; ∞)
6 sty 23:25
mat:
Rozwiązaniem jest suma tych przedziałów
odp: x∊[−1,5; ∞)
7 sty 01:24
Mila:
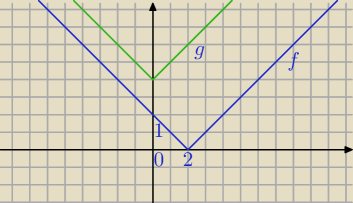
1)
|𝑥 − 2| − |𝑥| < 4⇔
|x−2|<4+|x|
f(x)=|x−2|
g(x)=|x|+4
x∊R
7 sty 01:47
kasia: ale ten 1 przyklad nie jest problemem tylko ten 2
7 sty 01:59
ABC:
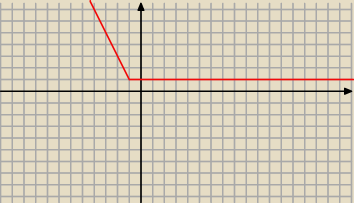
możesz też zauważyć że |x+1|−x jest zawsze dodatnia i pominąć zewnętrzną wartość bezwzględną
7 sty 08:21
Jolanta: Kasiu dobrze rozwiązałas drugi przyklad
7 sty 16:07
chichi:
w pierwszym nie trzeba robić przedziałami, wystarczy znać własności modułu

7 sty 16:47
kasia: ale ja podalam rozwiazanie z ksiazki z tylu a nie moje bo mi nie wychodzi wlasnie
7 sty 18:38
Jolanta: Tak zaczełas ?
|x+1|−x ≤2 i |x+1|−x≥−2
7 sty 18:50
kasia: no ale co dalej
7 sty 23:26
kasia: nie da sie tymi rysunkami z przedzialami
7 sty 23:26
baju-baju-baj:
1/ |x+1|−x ≤2 ∧ |x+1|−x≥ −2
dla x≥ −1
x+1−x≤2 ∧ x+1−x≥ −2
1≤2 ∧ 1≥−2
x∊ [−1,∞)
lub dla x<−1
−x−1−x≤2 ∧ −x−1−x≥ −2
−2x≤3 ∧ −2x≥ −1
x∊[−1,5; 0,5] ∧ x<−1
x∊[−1,5;−1)
suma przedziałów daje
odp: x∊[−1,5;∞)
7 sty 23:49
 1)
|𝑥 − 2| − |𝑥| < 4⇔
|x−2|<4+|x|
f(x)=|x−2|
g(x)=|x|+4
x∊R
1)
|𝑥 − 2| − |𝑥| < 4⇔
|x−2|<4+|x|
f(x)=|x−2|
g(x)=|x|+4
x∊R
 możesz też zauważyć że |x+1|−x jest zawsze dodatnia i pominąć zewnętrzną wartość bezwzględną
możesz też zauważyć że |x+1|−x jest zawsze dodatnia i pominąć zewnętrzną wartość bezwzględną
