 1. Z twierdzenia o reszcie wiemy że jeśli wielomian podzielony przez x − a daje resztę r, to
W(a) = r.
Dlatego jeśli reszta z dzielenia wielomianu W przez dwumian x − 1 ma być mniejsza od 3 to:
W(1) < 3
Dlatego podstawiamy 1 za x i powstaje nam nierówność kwadratowa
1 − m + m − 2 + 2 + m2 − 2 < 3
m2 − 4 < 0
(m − 2)(m + 2) < 0
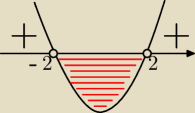
m = 2 ∨ m = −2
m∊(−2;2)
1. Z twierdzenia o reszcie wiemy że jeśli wielomian podzielony przez x − a daje resztę r, to
W(a) = r.
Dlatego jeśli reszta z dzielenia wielomianu W przez dwumian x − 1 ma być mniejsza od 3 to:
W(1) < 3
Dlatego podstawiamy 1 za x i powstaje nam nierówność kwadratowa
1 − m + m − 2 + 2 + m2 − 2 < 3
m2 − 4 < 0
(m − 2)(m + 2) < 0
m = 2 ∨ m = −2
m∊(−2;2)