planimetria bocian: Niestety nie poradziłem sobie z tym zadaniem bo okazuje się ze mam dwie niewiadome bo x=h−r i a tez nie mam. Na trójkącie równoramiennym o ramieniu pierwiastek z 8 opisano okrąg o promieniu 2.Oblicz długość podstawy tego trójkąta.

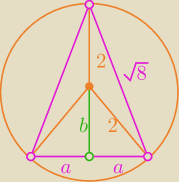
chichi: (1) b² + a² = 2² ⇒ a² = 4 − b² (2) (b + 2)² + a² = (√8)² b² + 4b + 4 + 4 − b² = 8 b = 0 wracamy do wyliczenia a dla b=0: a² = 4 ∧ a > 0 ⇒ a = 2 dłg. podstawy jest równa 2a = 4 P.S. nie chciało mi się już poprawiać rysunku, ale widzisz co się okazało

Aruseq: Jeśli jako α oznaczymy kąt między ramionami, a x podstawę trójkąta, to z twierdzenia sinusów i cosinusów otrzymamy:

x
	=4
sinα

x²=16−16cosα Wyliczamy x z pierwszego równania i podstawiamy do drugiego, otrzymując: 16sin²α=16−16cosα sin²α=1−cosα 1−cos²α=1−cosα cos²α−cosα=0 cosα=0 lub cosα=1 sprzeczność cosα=0, czyli α=90^o. W takim razie jest to trójkąt równoramienny prostokątny o przeciwprostokątnej długości 4.

bocian: dziękuje bardzo − rozumiem już