. Anonim123: W okrąg o promieniu 4 wpisano trójkąt równoramienny o kącie między ramionami 120stopni Oblicz stosunek pola koła wpisanego w ten trójkąt do pola koła opisanego na tym trójkącie.

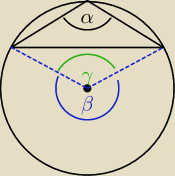
wredulus_pospolitus: Wersja rozwiązania dla TEGO KONKRETNEGO TRÓJKĄTA 1) Skoro kąt pomiędzy ramionami jest > 90^o, w takim razie trójkąt wygląda tak jak narysowany (środek okręgu nie zawiera się w trójkącie ) 2) Na mocy tw. o kącie wpisanym i środkowym, wiemy że β = 2*α = 240^o 3) Związku z tym γ = 360^o − β = 120^o = α 4) Zauważamy, że trójkąt o którym mowa w treści zadania, oraz trójkąt z kątem γ są trójkątami przystającymi (oba są równoramienne, mają ten sam kąt przy wierzchołku, więc mają takie same kąty, a że dzielą ze sobą tą samą podstawę, to znaczy że są to trójkąty przystające) 5) Związku z tym −−− trójkąt o którym mowa w treści zadania ma ramiona równe promieniowi okręgu.

	1		42
6) PΔ =		r*r*sinα =		*sin(120o) = ... dokończ
	2		2

wredulus_pospolitus: Wersja ogólniejsza. ad 1) tu nie będzie musiał zaistnieć (zresztą to było tylko po to by pokazać, że skąd ten rysunek) ad 2) mamy nadal ad 3) γ = 360 − 2α i teraz: 4) z tw. cosinusów wyznaczamy długość podstawy trójkąta: podstawa² = r² + r² − 2r²*cos(γ) 5) mając podstawę wracamy do naszego wyjściowego trójkąta i znowu korzystając z tw. cosinusów: podstawa² = bok² + bok² − 2*bok²*cos(α) wyznaczamy dzięki temu długość boku 6) i stosujemy ten sam wzór na pole trójkąta −−− i po ptakach Jak widzisz ... dzięki zauważeniu, że te dwa trójkąty są przystające, nie musieliśmy dwukrotnie się 'bawić' tw. cosinusów, tylko szybciutko napisaliśmy jaką długość będą miały ramiona wyjściowego trójkąta.