planimetria mała: Długości boków trójkąta są równe 4,5,7. Oblicz długość zawartego w tym trójkącie odcinka dwusiecznej najmniejszego kąta trójkąta.

Aruseq: Skorzystaj z twierdzenia o dwusiecznej

mała: czyli 4−x/x=5/7 x=7/3 i co teraz?

mała: pomocy

mała: i teraz z cosinusów?

Aruseq: Można z twierdzenia cosinusów

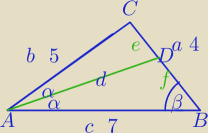
Mila: 1) I sposób Z tw. o dwusiecznej :

	5		7
e=		, f=
	3		3

W ABC: z tw. cosinusów 5²=4²+7²−2*4*7 cosβ

	5
cosβ=
	7

W ΔABD:

	7		7
d2=72+(		)2−2*7*		*cosβ
	3		3

	49		2*7*7		5
d2=49+		−		*		=
	9		3		7

	280
d2=
	9

2) II sposób Możesz skorzystać z twierdzenia: W każdym trójkącie iloczyn dwóch boków jest równy kwadratowi długości dwusiecznej kąta między nimi zawartego powiększonej o iloczyn odcinków , na które ta dwusieczna podzieliła trzeci bok. W Twoim zadaniu: c*b=d²+e*f⇔ d²=*b−e*f Z tw. o dwusiecznej :

	5		7
e=		, f=
	3		3

	5		7		1		280
d2=7*5−		*		=35*(1−		)=
	3		3		9		9

d=...? Posprawdzaj rachunki.

Mila: III sposób 1) Twierdzenie o dwusiecznej kąta 2) Skorzystaj z tw. Stewarta

mała: dziekuje