Optymalizacja
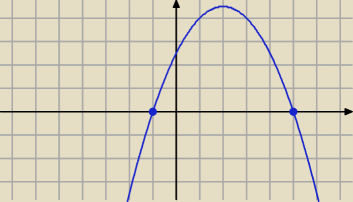
Nasiaa: Mamy fragment paraboli opisanej rownaniem y= −0,5(x−2)2 +4,5. Punkt P jest punktem wspólnym
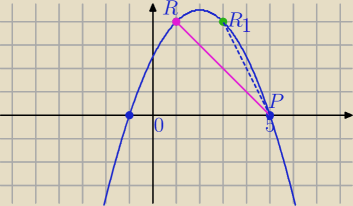
poraboli z osią Ox. Niech R będzie punktem leżącym na rozpatrywanym fragmencie paraboli
(I ćwiartka), a odległość R od P wyraża się wzorem
|PR| = √x44 −2x3 + 5x22+ 1254, gdzie x jest pierwszą współrzędną punktu R.
Wyznacz współrzędne takiego punktu R aby jego odległość od P była możliwie najwieksza. Oblicz
tę najwiekszą odległość.
28 gru 23:25
Aruseq: Z czym problem?
28 gru 23:29
Jolanta: wiesz jakie wspólrzedne ma P ?
29 gru 00:12
Asia:
Jakoś pytający nie potrafią określić w czym maja problem i mają problem z sformułowaniem
pytania
29 gru 00:38
Aruseq: Jeżeli chodzi o ruszenie tego zadania, to trzeba wyznaczyć współrzędne punktu P, następnie
uzależnić współrzędne punktu R od jednej zmiennej i następnie zastosować wzór na odległość
między punktami
29 gru 00:40
Jolanta: Nasiaa wiesz jak parabola ma ramiona?
29 gru 00:41
Jolanta: No cóz chyba się wstydzi pytać .Moze ktos ją kiedyś wysmiał
29 gru 00:47
Asia:
29 gru 00:50
Jolanta: y=−0,5(x−2)
2+4,5 z postaci kanonicznej przechodzimy na ogólną
y=−0,5(x
2−4x+4)+4,5
y=−0,5x
2+2x+2,5
| | 1 | | 5 | |
Δ=b2−4ac=22−4(− |
| )* |
| =9 |
| | 2 | | 2 | |
| | −b−√Δ | | −2−3 | |
X1= |
| = |
| =5 leży w pierwszej ćwiartce |
| | 2a | | | |
| | −b+√Δ | |
x2= |
| =−1 nie lezy w pierwszej cwiartce |
| | 2a | |
P=(5,0)
| | −1 | | 5 | |
R lezy na paraboli czyli dla dowolnego x y= |
| x2+2x+ |
| |
| | 2 | | 2 | |
odległosc miedzy punktem PiR |PR|=
√(xr−xp)2+(yr−yp)2
x
r=x x
p=5 y
p=0
|PR|=
√x−5)2+(y−0)2
|PR|=
√x2−10x+25+y2
29 gru 15:10
Jolanta: z tresci zadania |PR|=√x44−2x3+5x22+1254
29 gru 16:07
Aruseq: No i skoro punkt R leży na paraboli, to wiemy, że y=−0,5(x−2)2+4,5 − wystarczy podstawić
29 gru 17:42
Jolanta: własnie,ze wszystko mi sie zeruje
29 gru 17:44
Aruseq: jak się zeruje?
29 gru 17:44
Jolanta: Jezeli za y =−0,5.......podstawię do |PR|=
29 gru 17:52
Aruseq: | | 1 | | 1 | |
Przecież y2=(−0,5(x−2)2+4,5)2=(− |
| x2+2x+2,5)2= |
| x4−2x3+U{3} |
| | 2 | | 4 | |
|PR|=
√x2−10x+25+y2=
√14x4−2x3+52x2+1254
29 gru 18:06
Aruseq: | | 3 | |
Wkradł się błąd, miało być |
| x2 |
| | 2 | |
29 gru 18:06
Jolanta: Tak robiłam
29 gru 18:07
Jolanta: podnioslam obie strony do potegi 2
29 gru 18:09
29 gru 18:10
Jolanta: W treści zadania ?
29 gru 18:11
Mila:
x≥0
y= −0.5(x−2)
2 +4.5
−0.5(x−2)
2 +4.5=0
0.5(x−2)
2 =4.5 /*2
(x−2)
2=9
x−2=3 lub x−2=−3
x=5 lub x=−1
P=(5,0)
R=(x,−0.5(x−2)
2 +4.5)
|PR|=
√(x−5)2+(0.5(x−2)2 −4.5))2=
√0.25x4−2x3+2.5x2+31.25
sprawdziłam, bo
Jolancie co innego wyszło.
|PR|
2=0.25x
4−2x
3+2.5x
2+31.25
(0.25x
4−2x
3+2.5x
2+31.25)'=0.25*(x
3−6x
2+5x)
x*(x
2−6x+5)=0
x=0 lub x=1 lub x=5
maksimum dla x=1
d
maks(1)=
√32=4
√2
sprawdzajcie rachunki
29 gru 18:18
Jolanta: Mila dziękuję.Próbuje zrobic to zadanie ale wszystko mi sie sypie.|PR|2= 0,25x4−3x3....mam
tak
Ale co jest dalej ? Po lewej stronie pochodna z tego co wyzej .Po prawej przed nawiasem
dlaczego0,25
29 gru 19:52
Aruseq: Po prostu wyciągnęła 0,25 przed nawias, nie musisz tego robić
29 gru 21:12
Mila:
Mam policzyć po kolei pochodną?
29 gru 21:12
Jolanta: (0,25x4−2x3+2,5x2+31,25"=x3−6x2 +5x zapomniałam jak sie pisze 1 kreseczke
29 gru 21:18
Jolanta: Czy żle liczę pochodną ?
29 gru 21:22
Mila:
(0.25x4−2x3+2.5x2+31.25)'=x(x2−6x2+5)
Przez kopiowanie błędnie dopisałam 0.25
Przepraszam.. Nie wpłynęło to na rozwiązanie (na szczęście).
29 gru 21:23
Jolanta: To nic

Czy po ustaleniu x liczymy drugą pochodną ? Pierwsza=0 druga<0
29 gru 21:28
Mila:
1) Możesz liczyć drugą pochodną
2)
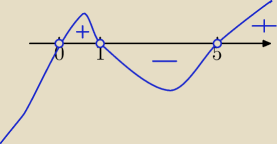
Ja badam jak pochodna f'(x) zmienia znak przy przejściu przez miejsca zerowe.
maksimum w x=1 bo f(x) z rosnącej zmienia się na malejącą
f(x) rosnąca dla f'(x) >0
f(x) malejąca dla f'(x)<0
Czasem liczenie drugiej pochodnej jest kłopotliwe.
30 gru 17:52
Jolanta: Dziękuję

30 gru 22:50

 x≥0
y= −0.5(x−2)2 +4.5
−0.5(x−2)2 +4.5=0
0.5(x−2)2 =4.5 /*2
(x−2)2=9
x−2=3 lub x−2=−3
x=5 lub x=−1
P=(5,0)
R=(x,−0.5(x−2)2 +4.5)
|PR|=√(x−5)2+(0.5(x−2)2 −4.5))2=√0.25x4−2x3+2.5x2+31.25
sprawdziłam, bo Jolancie co innego wyszło.
|PR|2=0.25x4−2x3+2.5x2+31.25
(0.25x4−2x3+2.5x2+31.25)'=0.25*(x3−6x2+5x)
x*(x2−6x+5)=0
x=0 lub x=1 lub x=5
maksimum dla x=1
dmaks(1)=√32=4√2
sprawdzajcie rachunki
x≥0
y= −0.5(x−2)2 +4.5
−0.5(x−2)2 +4.5=0
0.5(x−2)2 =4.5 /*2
(x−2)2=9
x−2=3 lub x−2=−3
x=5 lub x=−1
P=(5,0)
R=(x,−0.5(x−2)2 +4.5)
|PR|=√(x−5)2+(0.5(x−2)2 −4.5))2=√0.25x4−2x3+2.5x2+31.25
sprawdziłam, bo Jolancie co innego wyszło.
|PR|2=0.25x4−2x3+2.5x2+31.25
(0.25x4−2x3+2.5x2+31.25)'=0.25*(x3−6x2+5x)
x*(x2−6x+5)=0
x=0 lub x=1 lub x=5
maksimum dla x=1
dmaks(1)=√32=4√2
sprawdzajcie rachunki
 Czy po ustaleniu x liczymy drugą pochodną ? Pierwsza=0 druga<0
Czy po ustaleniu x liczymy drugą pochodną ? Pierwsza=0 druga<0
 1) Możesz liczyć drugą pochodną
2)
Ja badam jak pochodna f'(x) zmienia znak przy przejściu przez miejsca zerowe.
maksimum w x=1 bo f(x) z rosnącej zmienia się na malejącą
f(x) rosnąca dla f'(x) >0
f(x) malejąca dla f'(x)<0
Czasem liczenie drugiej pochodnej jest kłopotliwe.
1) Możesz liczyć drugą pochodną
2)
Ja badam jak pochodna f'(x) zmienia znak przy przejściu przez miejsca zerowe.
maksimum w x=1 bo f(x) z rosnącej zmienia się na malejącą
f(x) rosnąca dla f'(x) >0
f(x) malejąca dla f'(x)<0
Czasem liczenie drugiej pochodnej jest kłopotliwe.
