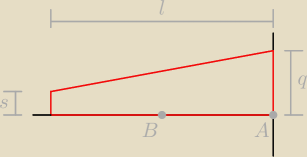
Środek ciężkości piotrek: Hej, jak znaleźć środek ciężkości takiej figury? Muszę znaleźć odległość od punktu A do B, gdzie B to współrzędna 'iksowa' środka ciężkości tej figury. Ktoś by pomógł? Bo w internecie nic nie mogę znaleźć na ten temat.

	1
Przykładowo gdyby ta figura była prostokątem, wtedy |AB|=		l.
	2

mat: https://bcpw.bg.pw.edu.pl/Content/3985/PDF/03SBPS20_srodek.pdf strona4, chodzi o fragment: Wynika stąd reguła: Dla znalezienia środka ciężkości trapezu należy więc poprowadzić a) prostą E F łączącą środki boków równoległych trapezu, b) prostą GH, którą otrzymamy odcinając na przedłużeniu boku górnego bok dolny, a na przedłużeniu dolnego górny — i łącząc otrzymane w ten sposób punkty G i H . Środek ciężkości leży na przecięciu lini EF i GH .

piotrek: Już działam, chwila

piotrek:

	2ql+sl		3l(q+s)		l(2q+s)
Wyszło mi, że |AB|=l−		=		−		=
	3(q+s)		3(q+s)		3(q+s)

	(q+2s)
=		l
	3(q+s)

Poprawnie?

HappyNewYear: Środek ciężkości dowolnej figury płaskiej możesz znaleźć, korzystając z tego, że:

	Sy		Sx
(xc, yc) = (		,		)
	A		A

gdzie S_y i S_x to momenty statyczne powierzchni względem odpowiednich osi, a A to pole powierzchni. Najprościej w przypadku takich figur podzielić to na prostsze figury (tu będzie to prostokąt i trójkąt), dla których znasz położenie środka ciężkości. Wynik dostałem taki sam, więc myślę, że jest zrobiłeś dobrze.