Proszę o pomoc w zad.: Wyznacz kąt w trójkącie wpisanym w kwadrat... Monika: W kwadrat ABCD wpisano trójkąt, który ma z tym kwadratem punkty wspólne DEF. Punkt E lezy na boku AB, a punkt F na boku BC. Kąt w trójkącie przy wierzchołku D ma 40 stopni, kąt DFC ma 80 stopni. Wyznacz kąt DEF. Wyznaczyłam kąty, które mogą mi się przydać, więc kąt CDF ma 10 stopni, kąt ADE ma 40 stopni, kąt AED ma 50 stopni. Zastosowałam własności kątów przyległych i doszłam układu równań z 4 niewiadomymi i po rozwiązaniu okazało się, że jest to układ nieoznaczony. I tu utknęłam.

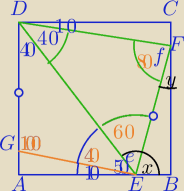
Mila: GE||DF

Monika: Dziękuję. Właśnie próbuję przeanalizować Twój tok rozumowania. Dzięki serdeczne

an:

Monika: Mila, w kącie f napisałaś 80 stopni, a to kąt DFC ma 80 stopni. To w takim razie chyba inaczej trzeba podążać...

Monika: an − o co pytasz?

Monika: Mila − Tak zgadza się, kąt f też będzie miał 80 stopni. Bardzo Ci dziękuję za pomoc Teraz to zad. wydaje się takie proste

Monika: Jeszcze mam pytanie. Jak doszłaś Mila do f=80. Bo to nie jest czworokąt wpisany w okrąg, kiedy suma przeciwległych kątów = 180 stopni. I czy z x, y , e , f tworzyłaś układ równań?

Monika: Nadal mnie Mila zastanawia ten kąt f=80 stopni, bo tylko w trapezie równoramiennym suma przeciwległych kątów = 180.

an: Upraszczanie tego będzie chyba wymagało sporo roboty

	DE2+EF2−DF2
cos∡DEF=		≈0,6286 ⇒ ≈ 51,053o
	2*DE*DF

Mila: Poczekaj

Monika: An, nie aż taką trudną metodą. Gdybym wiedziała, dlaczego na rys. DG=FE, to sprawa jest załatwiona, trapez DGEF byłby równoramienny, a wtedy kąty przeciwległe mają w sumie 180 stopni. I o to się sprawa rozbija

Mila: Spróbuję inaczej. Czekaj cierpliwie. Nie chcę korzystać z trygonometrii.

Monika: Dobrze Mila, bo mnie się już wszystkie pomysły wyczerpały. Dziękuję

Mila: błędnie założyłam równość pewnych odcinków. Chcę geometrycznie rozwiązać , o ile się da. Skąd masz to zadanie?

Monika: To jest zad. z olimpiady w Singapurze. Tylko nie umiałam tu wkleić obrazka, ale opis bezbłędnie odczytałaś.

an: Wynik nie jest "okrągły" a więc bez trygonometrii się raczej nie obędzie Powierzchnia trójkąta następnie wysokość z F na DE i otrzymujemy

	sin40
tg∡DEF=		⇒ ≈ 51,053o
	2sin40−sin50

Monika: An − też myślałam o tw. cosinusów, ale kiedy obejrzałam zad. koreańskie w podobnym stylu jak to, to oni dorysowują odcinki i tym sposobem znajdują rozwiązanie będące liczbą całkowitą..

an: można to zapisać też tak ctg∡DEF=2−tg50

an: tu rozwiązanie nie jest liczbą całkowitą, a ten drugi sposób bez tw cosinusów.

Monika: Gdyby udowodnić, że EF = GD, mielibyśmy zadanie rozwiązane, bo byłby tam trapez równoramienny. Może Mila coś wymyśli.

kaszojad: No właśnie jak się narysuje kątomierzem to wychodzi ∡f=90stopni

an: EF≠GD Jak udowodnić coś co jest nieprawdą, ja nie piszę szczegółowo rozwiązania tylko pewne wskazówki , bo jeśli ktoś ma rozwiązywać zadania z olimpiady to powinno mu wystarczyć

Monika: An − oczywiście. Wskazówki wystarczą. Tylko ja cały czas skłaniam się do tego, że rozwiązanie jest całkowite. Mila − cierpliwość jest cnotą króli

an:

	1		1
DE=		; DF=
	sin50		sin80

DE		sin(140−x)
	=
DF		sinx

ctgx=2−tg50

Monika: Dziękuję An. Tracę wiarę, że ten szukany kąt jest liczbą całkowitą

an: Matematyka jest nauka ścisłą opierającą się na faktach (czytaj obliczeniach, dowodach itp.) i wiara nie ma tu nic

Monika: Oczywiście, pełna zgoda, ale widziałam podobne zadania azjatyckie i tam sobie radzą geometrycznie. kreśląc różne pomocnicze linie. Podobnie jak Mila poprowadziła tą równoległą GE.

kaszojadka: a skąd Ty to zadanie wzięłaś (z jakiej strony)?

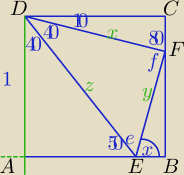
Mila: |AE|=tg(40^o) |CF|=tg(10^o)

	1−tg(10)
tg(x)=
	1−tg(40)

Nie jest to "ładny" kąt.

Monika: No właśnie, "ładny" nie jest Ja ten rysunek jeszcze zrobiłam od kątomierza, dorysowałam też różne inne proste równoległe i z własności kątów naprzemianległych i wierzchołkowych doszłam do tego, że ten szukany kąt ma 50 stopni. Kilka dni męczyłam to zadanie i już nie mam pomysłu. Tym bardziej, że nie znamy jego pełnej treści oraz tego, czy zaproponowano odpowiedzi w formie wyboru np. A. mniej niż 45 stopni, B. mniej niż 30, C. więcej niż 60, D. Około 50 stopni. Bardzo Wam dziękuję za wszelkie wsparcie.

an: Doszłaś Za te Twoje badania nagrody Abela nie dostaniesz ale Nobel czemu nie. Czy tak trudno na kalkulatorze sprawdzić moje rozwiązanie i porównać z @Mila gdzie szukany kąt DEF=180 −50−x

Monika: An, nie o to chodziło. Twoje rozwiązanie jest przy pomocy f. trygon. i ja go absolutnie nie neguję. Z kolei wg koncepcji Mili, jak rozwiązywałam układem równań, to mi wychodził nieoznaczony. Wiadomo, że ten kąt wynosi 50 lub 51 stopni, ale nie wiadomo, czy taka odp. byłaby do przyjęcia.

Monika: U mnie szukany kąt x= 40 +a. Gdybym udowodniła, że a=10 stopni, co jest bardzo prawdopodobne, to szukany x=50 stopni. Nie potrafię tu wykonać mojego skomplikowanego rysunku z dodatkowymi prostymi równoległymi, ale go dałam do googli i jest na tym linku: https://docs.google.com/presentation/d/1bcFRxdZJb41coXABjdPLwTdSGIsowMO003hm5s325Ak/edit#slide=id.p

an: Co to znaczy " Wiadomo, że ten kąt wynosi 50 lub 51 stopni, ale nie wiadomo, czy taka odp. byłaby do przyjęcia" Przy takich warunkach jak zostały podane w treści zadania ctg∡DEF=2−tg50 ⇒ 51,05324822...^o i nie widzę tu powodów do dyskusji, tym bardziej, że zgadza się to z rysunkiem w GeoGebrze z dokładnością 15 cyfr po przecinku

Monika: A jeśli jest to zad. na poziomie szkoły podst. kiedy uczniowie nie znają funkcji trygon., to też nie ma podstaw do rozwiązania go w inny sposób? Nie było podanej treści, był tylko rysunek, nie było wiadomo, czy to jest zad. zamknięte czy otwarte. Zostaw sobie to Twoje 51 stopni, ja tego rozwiązania przecież nie neguję. Ale także nie zamykam mu tej wg Ciebie jedynie słusznej drogi.

ite: https://ibb.co/cTQh7Rc kaszojadko to zadanie tak jak podała Monika pochodzi z SMO, jak chcesz poćwiczyć podobne, to skorzystaj z materiałów Singapore International Math Olympiad Challenge https://simoc.sg/sample-papers/

Monika: Ite, dziękuję Ci za ten link. Oprócz ciekawych zadań zauważyłam, że to są to zadania zamknięte (jeszcze nie sprawdziłam, czy wszystkie) i podanych jest 5 możliwych odpowiedzi od a) do e). Czyli mam rozwiązaną sprawę z tym trójkątem wpisanym w kwadrat, bo zapewne wśród wytypowanych odpowiedzi jest taka, że ten szukany kąt jest mniejszy niż 52 stopnie. Dziękuję wszystkim osobom, które dały mi wsparcie

ite: Część zadań to zadania otwarte np. https://sms.math.nus.edu.sg/download/sample_smo_questions.pdf

Mila: Wszystkim forumowiczom życzę spełnienia życzeń wigilijnych.