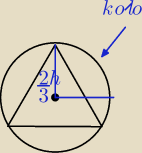
Trójkąt równoboczny - prawdopodobieństwo Mocher : Na trójkącie równobocznym opisano koło o promieniu R. W sposób losowy wybieramy punkt z wnętrza tego koła. Oblicz prawdopodobieństwo tego, że ten losowo wybrany punkt z wnętrza tego koła należy również do wnętrza trójkąta. Wskazówka:zależność wysokości trójkąta równobocznego h i

	2
promienia koła opisanego na tym trójkącie R jest dana wzorem R=		h
	3

wredulus_pospolitus: |Ω| = pole koła |A| = pole trójkąta

	|A|
P(A) =		=
	|Ω|

kaszojad:

kaszojad: @wredulus pospolitus @Mila @kerajs @Aruseq dobrze rozumiem?

	2h		4h2
P koła =π*(		)2 =π*
	3		9

P trójkąta=

	a√3
a(bok trójkąta) h=
	2

2h=a√3

	2h
a=
	√3

	2h   ( )2*√3   √3		4h2   *√3 3		h2*√3
P trójkąta		=		=
	4		4		3

π4h2   9		4π		4
	=		=		*√3*π
h2*√3   3		3√3		9

i to chyba jest odp?.:

4
	π√3
9

kaszojad: a nie to trzeba pole trójkąta podzielić na pole koła sorry

h2√3   3		3√3
	=		?
π4h2   9		4π

Mocher : Dziękuję serdecznie.

Piotrek : Chciałbym zadać może głupie pytanie odnośnie tego zadania ale pytam w kontekście przyszłego kolokwium, a dopiero się tego uczę. Czemu tutaj rozwiązano to zadanie przez poprzez policzenie pół trójkąta i koła. Czy da się to rozwiązać inaczej? Dzięki.

ABC: skoro się uczysz do kolokwium to aksjomatyczną definicję Kołmogorowa przyswoiłeś?

Piotrek : Pierwsze słyszę

Mocher : Nie. Ja też pierwszy raz słyszę.

ABC: ja się za was nie nauczę

Mocher : Ok. W porządku. Dzięki

kaszojad: https://pl.wikipedia.org/wiki/Przestrze%C5%84_probabilistyczna

kaszojad: to jest to?

chichi: tak.

kaszojad:

Mocher : Dziękuję