Wzór Bayesa SEBA: Drobna pomoc z prawdopodobieństwa. Przed egzaminem ogłoszono listę 150 pytań z dziedziny A, 100 z B oraz 50 z C. Student potrafi odpowiedzieć na 50 pytań z A , 25 pytań z B oraz na wszystkie z C. a) Oblicz prawdopodobieństwo zdarzenia, że podczas egzaminu odpowie na losowo zadane pytanie. b) Jakie jest prawdopodobieństwo, że wylosował pytanie z dziedziny A jeśli wiadomo że zdał egzamin? Podczas egzaminu zadano mu 1 pytanie.

er: X − student zdał egzamin P(X)=P(X|A)*P(A) + P(X|B)*P(B) + P(X|C)*P(C)

	50		150		25		100		50
P(X)=		*		+		*		+1*
	150		300		100		300		300

SEBA: To jest do podpunktu a?

er: P(A|X)=P(X|A)*P(A)/P(X)=P(X|A)*P(A)

er: Tak

SEBA: Dziękuję. A dare radę b? Nie jestem niestety dobry w te klocki. Dziękuję.

er: b) też rozpisałem, wystarczy podstawić

SEBA: Czy tu trza zastosować wzór bayesa?

SEBA: Czy do podpunktu b stosujemy może wzór Bayesa

wredulus_pospolitus: A po kiego grzyba?

	3*1/3
b) P(A|Zdał) =
	3*1/3 + 2*1/4 + 1

albo jeszcze prościej zapisać:

	50
P(A|Zdał) =
	50+25+50

SEBA: No i to jest konkret. Wielkie dzięki.

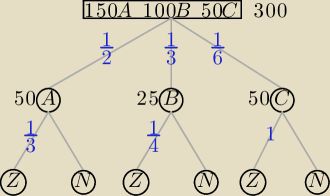
CBA: To samo z nieśmiertelnym drzewkiem Z − zda, N − nie zda

	1		1		1		1		1
a) P(ZDA) =		*		+		*		+		* 1
	2		3		3		4		6

	1   1   *   2   3
b) P(A|ZDA) =
	1   1   1   1   1   * + * + *1 2   3   3   4   6