Oblicz pole podstawy KUBA S: Przekątna graniastosłupa prawidłowego czworokątnego ma długość 8 cm i jest nachylona do podstawy pod kątem 45 stopni. Pole podstawy tego graniastosłupa jest równe :

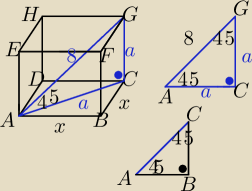
kaszojad: może rysunek tego nie oddaje, ale: z pitagorasa a²+a²=8² 2a²=64 a²=32 a=√32=4√2 Trójkąt ABC to trójkąt 45,45,90, w którym przeciwprostokątna to x√2 (x to długość boku kwadratu ABCD) a=x√2=8 x√2=8

	8		8		√2
x=		=		*		=4√2
	√2		√2		√2

Ponieważ podstawa to kwadrat, więc Pp =(4√2)²=32cm²

Mila: a=4√2 to x=4 2) Nie musiałeś liczyć a.

	a2
P□=		( liczymy jak w rombie)
	2

P_□=16

kaszojad: oki

kaszojad: czyli ja pomyliłam (nie wiem dlaczego napisałam, że a =8?) bo skoro a =x√2, a=4√2 to x=4

KUBA S: to jakie jest prawidłowe rozwiązanie

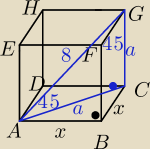kaszojad: trójkąt ACG jest prostokątny równoramienny 90,45,45 z Pitagorasa a²+a²=8² 2*a²=64 a²=32 a=√32=4√2 ponieważ podstawa jest kwadratem, a |AC| to przekątna tego kwadratu i dzieli go na dwa przystające trójkąty prostokątne równoramienne z zależności trójkąta 45, 45, 90 przeciwprostokątna to x√2 x√2=4√2=a x=4 Pp=4²=16