Oblicz objętość graniastosłupa KUBA S: Wysokość graniastosłupa prawidłowego czworokątnego jest równa √119. Przekątna tego graniastosłupa i przekątna jego ściany bocznej, wychodzące z jednego wierzchołka, tworzą kąt którego tangens jest równy ⁵₁₂≠. Oblicz objętość tego graniastosłupa

Aruseq: wynik to ≈π

KUBA S: Czyli ? bo nie rozumiem

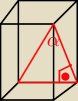
Aruseq: Tangens tego kąta odpowiada stosunkowi długości boku podstawy do długości przekątnej graniastosłupa. Możesz je dzięki temu od siebie uzależnić. Natomiast przekątna ściany bocznej zależy od krawędzi podstawy i od wysokości graniastosłupa, mając wysokość możesz wyliczyć krawędź podstawy. A tamta wiadomość wyżej nie pochodzi ode mnie, ktoś ustawił sobie taki nick jak ja