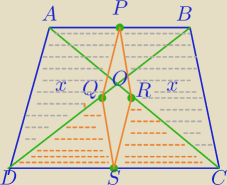
trapez gwint: ABCD to trapez, w którym AB||CD. P, Q, R, S to odpowiednio środki AB, BD, DC, CA. AC i BD przecinają się w punkcie O. Pole trójkąta AOB = 2019 i pole trójkąta COD = 2020. Jakie jest pole czworokąta PQRS?

Mila: Podpowiedź: x=P_ΔAOD=P_BOC 1) PABCD=2019+2020+2x 2) P_ABCD=2019+2020+2x

	3
PAPQD=		PΔABD
	4

	3		1
PPQRS=PABCD−[2*		PΔABD+2*		PDCA]
	4		4

an:

	a−b		P2   a(1−√ )   P1
QR=		=		}}
	2		2

	P2
PS=h=h1+h2=h1(1+√		)
	P1

	QR*PS		P2   a(1−√ )   P1		P2
PP−Q−R−S=		=		*h1(1+√		)
	2		2*2		P1

	a*h1		P2		P2		P1−P2
PP−Q−R−S=		(1−√		) (1+√		)=
	2*2		P1		P1		2

	P1−P2
PP−Q−R−S=
	2

	2020−2019		1
PP−Q−R−S=		=
	2		2

an: jakiś chochlik Pp−Q−R−S oczywiście powinno być P_PQRS

Mila: Zgadza się z moim wynikiem. Jednak gwinta już to nie interesuje.