geometria analityczna, trójkąt, współrzędne punktów vol: Trójkąt ABC jest trójkątem równoramiennym, którego podstawa AB zawarta jest w prostej o równaniu y = −x + 3. Ramię AC trójkąta zawiera się w prostej o równaniu y = 2x + 6, a do ramienia BC należy punkt D = (−1,10) Oblicz współrzędne punktów A, B i C

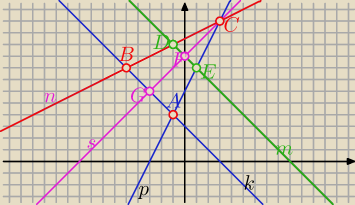
Eta: A(−1,4), B(−5,8) , C(3,12) =====================

	⎧	y=−x+3
1/	⎩	y= 2x+6	⇒ A=(−1,4)

======== 2/ m || k i D∊k ⇒ m: y= −x+9

	⎧	y= −x+9
3/	⎩	y=2x+6	⇒ E(1,8) to F(0,9) −− środek odcinka DE

4/ prosta s⊥AB i F∊ s to s : y= x+9

	⎧	y=x+9
5/	⎩	y=−x+3	⇒ G (−3,6) −− środek odcinka AB

to B(−5,8) ==========

	⎧	y=2x+6
6/	⎩	y=x+9	⇒ C(3,12)

========

vol: dziekuje