Podobieństwo trójkątów MaciekMarcula: Na prostokącie CDEF o wymiarach 8x1 opisano trójkąt prostokątny ABC w sposób przedstawiony na rysunku. Dwa sąsiednie boki prostokąta CDEF zawierają się w przyprostokątnych trójkąta ABC, a wierzchołek nienależący do tych boków leży na przeciwprostokątnej. Zdjęcie poglądowe oraz to do czego samemu doszedłem wrzucam tutaj: https://imgur.com/WY9Efzv Wyznacz najmniejszą długość jaką może mieć przeciwprostokątna trójkąta ABC

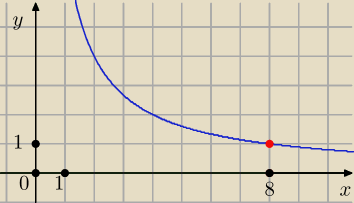
a7: Przeciwprostokatna tropjkata ABC jest proporcjonalna do przeciwprostokatnej trójkąta ADE i gdy AE będzie miało najmniejsza długość to i AB będzie najkrótsze FB=x FC=1 ED=1 AD=8/x (z podobieństwa trójkątów EFB i AED) AE będzie najmniejsze gdy AD będzie najmniejsze gdyż AE=√1²+AD² załx.>1 i x≤8 iloraz 8/x jest najmniejszy dla x=8 równy 1 AE=√2 EB= 8√2 AB=9√2

a7:

a7: niestety to jest źle

ite: MaciekMarcula taka uwaga do rozwiązania zad.13.1 czy warunek x>0, który tam podałeś jest prawidłowy, czy zgadza się z rysunkiem?

ite: *źle spojrzałam na rysunek, warunek jest oczywiście poprawny

ite: Przeciwprostokątna Δ ABC będzie mieć najmniejszą długość, gdy wyliczona w zad.13.1 funkcja wyrażająca jej długość będzie mieć minimum. Oczywiście ma być to minimum z przedziału, w którym zawierają się możliwe długości odcinka AB. Czyli pozostaje znaleźć to minimum.

klocuch22: W jaki sposób mogę obliczyć minimum tej funkcji? I jakim przedziałem będą te możliwe długości odcinka AB. Niestety nie rozumiem dalej tego zagadnienia

ite: Długość przeciwprostokątnej AB w zależności do długości odcinka x [gdzie x∊(0,+∞)] opisuje funkcja: f(x) = √(x+1)²+64*(x+1)²*1/x² ↑ (jedyny sposób zapisu, który nie 'wyskoczył' spod pierwiastka) Funkcja pierwiastka kwadratowego jest funkcją ściśle monotoniczną → rosnącą, więc najmniejszą wartość funkcji otrzymamy, gdy wstawimy do wzoru najmniejszą wartość pod pierwiastek. To znacznie ułatwia liczenie, bo wystarczy dalej analizować tylko funkcję podpierwiastkową. Badana funkcja f(x) (więc również długość przeciwprostokątnej) będzie mieć najmniejszą wartość,

	64*(x+1)2
gdy funkcja (x+1)2+		przyjmie wartość najmniejszą.
	x2