Wyznaczanie wartości parametru m Maciek21: Dane jest równanie z niewiadomą x : x² +mx+m−2 = 0 Wyznacz wszystkie wartości parametru m dla których to równanie ma dwa różne pierwiastki x₁ i x₂ takie że wyrażenie (3x₁ + 4x₂)² + (4x₁ −3x₂)² przyjmuje najmniejszą wartość.

Maciek21: Wykorzystywałem wzory viete'a ale delta non stop wychodzi ujemna czy podstawie pod p czy pod q wierzchołka

ABC: jak ty to liczysz ? Δ=m²−4(m−2)=m²−4m+8=m²−4m+4+4=(m−2)²+4 więc jest zawsze dodatnia a nie ujemna

Aruseq: Ale delta tego wyrażenia niekoniecznie musi być większa od zera

Aruseq: Możliwe ze chodziło mu o deltę z tego wyrażenia z x₁ i x₂

Aruseq: O ile się nie mylę, odpowiedz to m=1

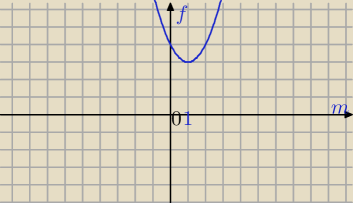
Mila: 1) x² +mx+m−2 = 0 Δ=m²−4*(m−2)=m²−4m+8 m²−4m+8>0 Δ_m=16−32<0⇔ dla każdego m∊R równanie ma dwa różne rozwiązania 2) x₁+x₂=−m, x₁*x₂=m−2 f(x₁,x₂)=(3x₁ + 4x₂)² + (4x₁ −3x₂)² =9x₁²+24x₁x₂+16x²+16x₁²−24x₁*x₂+9x₂² f(x₁,x₂)=25x₁²+25x₂²=25(x₁²+x₂)²=25*[(x₁+x₂)²−2x₁*x₂] f(m)=25[(−m)²−2(m−2)]=25*(m²−2m+4) Wsp. wierzchołka paraboli (skierowanej do góry)

	−(−2)
p=		=1
	2

Ta funkcja kwadratowa ma najmniejszą wartość w wierzchołku, czyli dla m=1 3) dla m=1 wyrażenie (3x₁ + 4x₂)² + (4x₁ −3x₂)² ma najmniejszą wartość