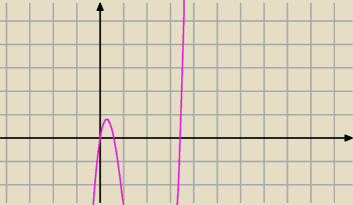
monotonicznosc czech: czy funkcja (3/4)x⁴ − 4x³ + 3x² −5 jest monotoniczna w przedziale <√2 −2 : 3>

eM: Na pewno dobrze przepisales granice przedziału?

chichi: a co Ci nie gra z tym przedziałem?

eM: Obecnie odpowiedz to nie, bo dla ciągu −1/2, 0, 1/2 mamy odpowiednio wartosci −237/64, −320/64, −301/64, więc funkcja nie jest monotoniczna w tym przedziale. Jesli w tresci natomiast byłoby 2−√2 to wtedy odpowiedź jest inna.

czech: no wlasnie o to mi chodzi bo sa przedzialy a (− nieskonczonosc : 0> b <0: √2 −2 > c <√2 −2 : 3> d <3: nieskonczonosc) i w ksiazce jest d i w takich rozwiazaniach d ale ja tu widze ze c tez pasuje bo pochodna zmienia znak w przedziale

chichi: b. od kiedy tak zapisujemy przedziały

chichi: co to za książka

chichi: odp. A jest poprawna poza tym

eM: Błąd w ksiązce pewnie, a) pasuje

chichi:

	3
f: R → R dana jest wzorem f(x) =		x4 − 4x3 + 3x2 − 5, wówczas:
	4

f'(x) = 3x³ − 12x² + 6x = x(3x² − 12x + 6) f'(x) < 0 ⇔ x ∊ (−∞,0) ∪ (2 − √2, 2+√2), zatem: funkcja f jest malejąca na przedziale (−∞,0) oraz na przedziale (2 − √2, 2+√2) weźmy teraz funkcję g, taką że:

	3
g: (−∞,0) → R daną wzorem g(x) =		x4 − 4x3 + 3x2 − 5, wówczas
	4

∀x∊D_g ( f'(x) < 0 ), a stąd wynika, że funkcja jest malejąca na całej swojej dziedzinie, zatem jest monotoniczna

czech: znaczy pytanie jest w ktorym jest nie monotoniczna

...: XDD