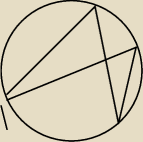
 Punkty ABCD leżą na okregu. s tego okręgu lezy na odcinku AC.Długość cięciwy BC jest równa
promieniowi oktegu.
Wtedy:
Miara kąta acb jest rowna 60
Miara kąta abd jest mniejsza niz 60
A na dole D jest naprzeciw A
C i B cieciwa
Punkty ABCD leżą na okregu. s tego okręgu lezy na odcinku AC.Długość cięciwy BC jest równa
promieniowi oktegu.
Wtedy:
Miara kąta acb jest rowna 60
Miara kąta abd jest mniejsza niz 60
A na dole D jest naprzeciw A
C i B cieciwa


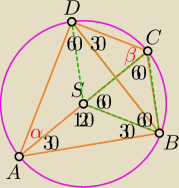 uzupełniamy rysunek korzystając z tw. o kątach wpisanych i środkowych opartych na tym samym
łuku, a następnie zauważamy, że:
|∡ADC| = 90o = |∡ABC|, z ΔADC: α + β = 90o, wiemy, że ABCD − opisany na okręgu, zatem mamy
też, że: a + 30o = β + 60o, łącząc te 2 warunki mamy: α = 30o i β = 60o, stąd:
|∡ACB| = 60o (ok) oraz |∡ABD| = 60o (nie jest mniejsze od 60o)
uzupełniamy rysunek korzystając z tw. o kątach wpisanych i środkowych opartych na tym samym
łuku, a następnie zauważamy, że:
|∡ADC| = 90o = |∡ABC|, z ΔADC: α + β = 90o, wiemy, że ABCD − opisany na okręgu, zatem mamy
też, że: a + 30o = β + 60o, łącząc te 2 warunki mamy: α = 30o i β = 60o, stąd:
|∡ACB| = 60o (ok) oraz |∡ABD| = 60o (nie jest mniejsze od 60o) 