Prawdopodobieństwo
Natalia: Prawdopodobieństwo
Proszę o wyjaśnienie: Na ile sposobów można ustawić 10 osób w szereg tak aby ustalone dwie
osoby nie stały obok siebie ?
Ustawienia, w których dwie ustalone osoby stoją obok siebie:
2!⋅8!⋅9=2⋅9!
Dlaczego tak? Nie rozumiem dlaczego jeszcze mnoży się razy 9
Wiem że potem to się odejmuję od liczby wszystkich możliwych ustawień czyli 10! Rozumiem że 2!
dlatego że możemy te osoby ustawić w każdym miejscu na dwa sposoby i każdy z pozostałych osób
ma możliwości 8! ale dlaczego *9?
30 lis 18:44
Aruseq:
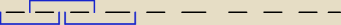
Ta 9 wynika z tego typu łączenia miejsc w pary. 10 miejsc możemy połączyć w 9 takich par, czyli
te dwie osoby mogą usiąść obok siebie na 9 różnych parach miejsc. 2! wynika z tego, że te 2
osoby mogą się między sobą mieszać, a 8!, gdyż pozostałe osoby też mogą się zamieniać
miejscami
30 lis 18:47
Mila:
Możesz rozumować w taki sposób:
(A,B) − dwie ustalone osoby traktujesz jako jeden "scalony" element,
w takim razie masz do ustawienia 9 różnych elementów
stąd
2!*9! − liczba takich ustawień , że osoby A i B stoją obok siebie.
30 lis 21:43
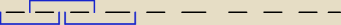 Ta 9 wynika z tego typu łączenia miejsc w pary. 10 miejsc możemy połączyć w 9 takich par, czyli
te dwie osoby mogą usiąść obok siebie na 9 różnych parach miejsc. 2! wynika z tego, że te 2
osoby mogą się między sobą mieszać, a 8!, gdyż pozostałe osoby też mogą się zamieniać
miejscami
Ta 9 wynika z tego typu łączenia miejsc w pary. 10 miejsc możemy połączyć w 9 takich par, czyli
te dwie osoby mogą usiąść obok siebie na 9 różnych parach miejsc. 2! wynika z tego, że te 2
osoby mogą się między sobą mieszać, a 8!, gdyż pozostałe osoby też mogą się zamieniać
miejscami