koło Luz: Oblicz pole największego możliwego koła, które można wpisać w czworokąt ABCD taki, że AB=14cm, BC=9cm, CD=7cm i DA=12cm .

wmboczek: Twierdzenie Bretschneidera dwa przeciwległe kąty muszą dawać 180 stopni jest to możliwe dla cosa=1/5 chyba P=24π

Luz: Czy pole ABCD = 41*24+54

an: Pole koła jest max dla max powierzchni ABCD wynika to ze wzoru na R wpisane z kolei ABCD osiąga max jak podał zgodnie z twierdzeniem, które podał @wmboczek P=√7*12*14*9 dalej wzór na R wpisane

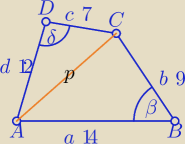
Mila: 1) W czworokąt ABCD o bokach j.w. można wpisać okrąg. a+c=21=b+d 2) Ze wszystkich czworokątów o danych bokach ( następujących po sobie w określonej kolejności ) największe pole ma czworokąt wpisany w okrąg− taki czworokąt istnieje tylko jeden . w zadaniu boki: 14,9,7,12. 3) Pole czworokąta wpisanego w okrąg i opisanego na okręgu : P=√a*b*c*d 4) Zakładając, że czworokąt ABCD jest wpisany w okrąg : z tw. cosinusów mamy:

	a2+b2−c2−d2
cosβ=
	2(ab+cd)

	1
i cosβ=		jak podał wmboczek
	5

Można zatem obliczyć pole czworokąta ABCD wpisanego w okrąg i promienie obu okręgów.