geometria analityczna wojtek B: Środek ciężkości trójkąta o wierzchołkach A(−10, −7) B( −3,−4) C(1,5) akie ma współrzędne

wojtek B: Obliczyłem srodek boku AB i ma wspórzedne punt D (−6,5 i −5,5)

wojtek B: nie wiem co dalej

Mariusz: Napisz równanie prostej CD Jeszcze potrzebujesz równanie drugiej prostej którą znajdujesz analogicznie

Mila: 1)

	a1+b1+c1		a2+b2+c2
S(x,y)=(		;		)− wsp. środka ciężkości Δ o wierzchołkach:
	3		3

A=(a₁,a₂),B=(b₁,b₂) , C=(c₁,c₂) 2) A=(−10, −7), B=( −3,−4) , C=(1,5)

	−10+(−3)+1		−7+(−4)+5
S(xs,ys)=(		,		)=(−4,−2)
	3		3

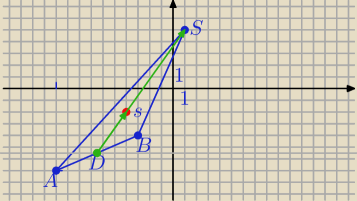
II sposób D=(−6.5,−5.5) −środek boku AB DC^→=[7.5,10.5]

	1
DS→=		[7.5, 10.5]=[2.5, 3.5]
	3

D=(−6.5,−5,5)→T_{[2.5, 3.5]}⇒S=(−6.5+2.5; −5.5+3.5]=(−4,−2)

chichi: jeżeli S jest środkiem ciężkości trójkąta tzw. barycentrum, to

	xA+xB+xC		yA+yB+yC
S = (		,		)
	3		3

wojtek B: Dziekuje