dowód z geometrii Alaias: Dany jest czworokąt wypukły ABCD o długościach boków a, b, c, d i P to jego pole, Udowodnij, że P<= 1/4( a+b+c+d )

chichi: kwadrat o boku długości równej 2, ma pole i obwód równe odpowiednio 4 i 8, sprawdźmy:

	1
4 ≤		(8), a to oznaczałoby, że 4 ≤ 2 − no to chyba nie ma co dowodzić
	4

Alaias: No, tak miało być P<=1/4 (a²+b²+c²+d²) :(

chichi:

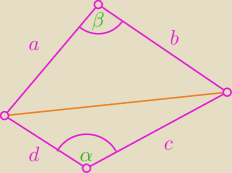
	1		ab + cd		a2 + b2   c2 + d2   + c2   2
S =		(absin(β) + cdsin(α)) ≤		≤		=
	2		2		2

	1
=		(a2 + b2 + c2 + d2) □
	4

chichi:

	a2 + b2
tam w ostatniej nierówności wkradł się chochlik powinno oczywiście być
	2

Alaias: Dzięki