dane są punkty
Julek : Dane są punkty: A (−4, − 1), B (3, − 5), C (2, 3), D (−6, 2).
Wykaż, że trójkąt: a) ABC jest równoramienny, b) ADC jest prostokątny.
22 lis 21:58
Aruseq: a) Policzyć długości wszystkich boków trójkąta, pewne dwa powinny wyjść równej długości
b) Albo wyznaczyć równania prostych, na których leżą boki trójkąta i wtedy wskazać parę
prostych równoległych, albo skorzystać z prostopadłości wektorów
22 lis 22:05
chichi:
(b) albo też policzyć długości boków i pokazać, że zachodzi tw. Pitagorasa

22 lis 22:18
chichi:
"wtedy wskazać parę prostych równoległych"
prostopadłych ** 
22 lis 22:19
Mariusz:
a) można sprawdzić czy jeden z wierzchołków leży na symetralnej boku
ciekawe czy to wystarczy
b) można sprawdzić czy jeden z wierzchołków leży na okręgu o środku w środku odcinka
i promieniu równym połowie tegoż odcinka
23 lis 02:05
Mila:
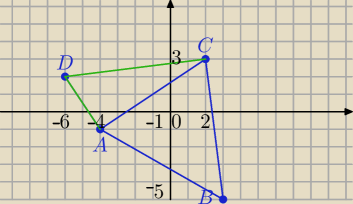
A (−4, − 1), B (3, − 5), C (2, 3), D (−6, 2).
1)
|AB|=
√72+42=
√65
|BC|=
√12+82=
√65
|AB|=|BC|
ΔABC− Δrównoramienny
2) Dalej w podobny sposób oblicz długości AC, AD, DC i z tw. odwrotnego
do tw. Pitagorasa sprawdzasz czy ΔADC jest prostokątny
albo
tak:
AC
→=[6,4]
AD
→=[−2,3]
[6,4] o [−2,3]=−12+12=0⇔wektory są prostopadłe.
AD⊥AC
ΔADC− Δprostokątny.
23 lis 16:41


 A (−4, − 1), B (3, − 5), C (2, 3), D (−6, 2).
1)
|AB|=√72+42=√65
|BC|=√12+82=√65
|AB|=|BC|
ΔABC− Δrównoramienny
2) Dalej w podobny sposób oblicz długości AC, AD, DC i z tw. odwrotnego
do tw. Pitagorasa sprawdzasz czy ΔADC jest prostokątny
albo
tak:
AC→=[6,4]
AD→=[−2,3]
[6,4] o [−2,3]=−12+12=0⇔wektory są prostopadłe.
AD⊥AC
ΔADC− Δprostokątny.
A (−4, − 1), B (3, − 5), C (2, 3), D (−6, 2).
1)
|AB|=√72+42=√65
|BC|=√12+82=√65
|AB|=|BC|
ΔABC− Δrównoramienny
2) Dalej w podobny sposób oblicz długości AC, AD, DC i z tw. odwrotnego
do tw. Pitagorasa sprawdzasz czy ΔADC jest prostokątny
albo
tak:
AC→=[6,4]
AD→=[−2,3]
[6,4] o [−2,3]=−12+12=0⇔wektory są prostopadłe.
AD⊥AC
ΔADC− Δprostokątny.